Matematika Maja

Na prostoru Mezoamerike, regiona Severne Amerike koji se prostire od centralnog Meksika do granice s južnom Amerikom, pre dolaska Еvropljana razvilo se nekoliko različitih civilizacija. Najznačajnije su civilizacije naroda Olmeka, Zapoteka, Maja, Mišteka, Tolteka i Asteka. Sve mezoameričke civilizacije su imale niz zajedničkih osobina. Tako su, na primer, sve pobrojane civilizacije su imale šamansku religiju, agrokulturu zasnovanu na kukuruzu, dva kalendara, piktografsko pismo, vigezimalni¹ brojevni sistem, itd...

Civilizacija Maja je od svih Mazomeričkih civilizacija najduže trajala i dostigla najveći stepen razvoja u svim pogledima. U nastavku rada ćemo kratko opisati istoriju civilizacije Maja a zatim i matematiku i astronomiju ove mezoameričke civilizacije.

Civilizacija Maja

Civilizacija Maja se razvila na prostoru poluostrva jukatan (slika 1). Teritorije nekadašnje civilizacije danas pripadaju današnjim državama Meksikio, Gvatemala, Beliz, Honduras i Еl Salvador.

Istorija civilizacije Maja, kao i istorija ostalih Mezoameričkih civilizacija, može se podeliti na tri razdoblja:

1. Preklasični period – od 2500. godine pre nove ere do III veka nove ere,
2. Klasični period – od III veka do IX veka,
3. Postklasični period – od IX veka do XVI veka.

Španski kolonisti su u XVI veku pokorili Mezoameričke narode, uključujući Maje i Asteke. Katolički misionari koji su došli u Mezoameriku zajedno sa Španskim osvajačima, nametnuli su hrišćanstvo starosedocima Mezoamerike. Na veliku žalost, tom prilikom je došlo do velikog gubitka kulturnog nasleđa Maja. Hramovi Maja i knjige su uništeni, a religija i pismo Maja zabranjeni.

Do danas su sačuvane samo četiri knjige Maja, takozvani kodeksi (Grolier Codex, Dresden Codex, Troano Codex i Paris Codex), sve četiri napisane u postklasičnom periodu. Kako je pismo Maja odavno bilo zabranjeno, krajem devetnaestog veka ih niko nije mogao pročitati. Tokom dvadesetog veka, pismo Maja je uspešno dešifrovano zajedničkim naporom mnogih naučnika, i danas se smatra jedinim dešifrovanim pismom Mezoameričkih civilizacija².

Pismo Maja se sastoji od logograma³ kao i od silabograma⁴. Logogrami su uglavnom bile detaljne slike stvari koje simbolišu (na primer logogram za reč „majmun“ bi bila slika majmunske glave), dok su silabogrami češće imali apstraktniju (prostiju) formu. Silabogrami su se mogli dodavati na logograme ili na druge silabograme u svrhu formiranja novih simbola ili menjanja značenja postojećim (videti sliku 2). Takva kombinovanja simbola nisu se povijala strogim pravilima, već bi autor teksta imao prostora da izrazi svoju likovnu kreativnost. Do sada je ukupno identifikovano oko 1000 različitih simbola koje su Maje koristile za pisanja, međutim većina njih je nastala kombinovanjem manjeg broja simbola. Maje su tekstove pisale u dvostubičastim kolonama sleva na desno, odozgo ka dole.

Brojevni sistem

Kao i ostali Mezoamerički narodi⁵, Maje su koristile brojevni sistem s osnovom 20. Ono što razlikuje Maje od nekih drugih Mezoameričkih naroda (kao na primer Asteka), je to što su Maje koristile pozicioni brojevni sistem i cifru nula. Maje su počele da koriste ovakav sistem u preklasičnom periodu, najverovatnije preuzimajući ga od Olmeka⁶.

U brojevnom sistemu Maja, nula se označava školjkom, dok se ostale cifre dobijaju kombinacijom tačkica (koje imaju vrednost 1) i crtica (koje imaju vrednost 5). Sve cifre su prikazane u narednoj tabeli:

Maje su cifre nekog broja zapisivali odozgo ka dole, tako da prva cifra ima najveću vrednost. Na primer, oznaka

u vigezimalnom sistemu s Majanskim ciframa predstavlja broj $12\times {20}^2+16\times 20+5=5125$.

Sabiranje i oduzimanje pojedinačnih cifara (brojeva manjih od 20) veoma je jednostavno u brojevnom sistemu Maja. Na primer, prilikom sabiranja, dovoljno je crtice i tačkice dve cifre spojiti u jednu novu cifru:

Pritom, ako se tim kombinovanjem pojavi više od pet tačkica, tada se pet tačkica zamenjuju jednom crticom, a ako se pojavi više od četiri crtice tada se one zamenjuju nulom, a jedna tačkica se dodaje u viši red:

Prilikom oduzimanja iz većeg broja se uklanjaju crtice i tačkice manjeg broja:

Pritom, ako u većem broju ne postoji dovoljno tačkica, onda se jedna od crtica pretvara u pet tačkica, a ako u većem broju ne postoji dovoljno crtica tada se jedna od tačkica iz višeg reda pretvara u pet crtica.

Sabiranje i oduzimanje višecifarnih brojeva se vrši ponavljanjem opisanih postupaka, analogno načinu sabiranja i oduzimanja brojeva u decimalnom zapisu. Iako bi i množenje i deljenje brojeva moglo lako da se vrši postupcima nalik na one za decimalni sistem (videti, na primer, [1]), do sada nisu pronađeni nikakvi dokazi da su Maje vršile množenje i deljenje. Takođe, ne postoje dokazi da su Maje koristile negativne brojeve, razlomke ili nešto nalik na decimalnu tačku.

Sudeći po sačuvanim knjigama Maja i natpisima uklesanim u zidovima hramova, Maje nisu koristile pravi pozicioni sistem s osnovom 20 već jednu modifikaciju takvog sistema. Naime, u brojevnom sistemu koji se koristi na pomenutim mestima, prva cifra odozdo „poseduje težinu“ $1$, druga cifra „poseduje težinu“ $20$, dok treća cifra „poseduje težinu“ $360=18\times 20$ a ne ${20}^2$ kao u „pravom“ vigezimalnom sistemu. Četvrta cifra „poseduje težinu“ $18\times {20}^2$, peta $18\times {20}^3$, itd... Drugim rečima, vrednost broja sa zapisom

je

Prema tome, oznaka (1) ne predstavlja vrednost $5125$ već $12\times 18\times 20+16\times 20+5=4645$.

Maje su najveravatnije koristile ovakav brojevni sistem da bi lakše radili s kalendarom (pogledati narednu sekciju). Neki autori smatraju da su modifikovani vigzemalni sistem koristili samo sveštenici za astronomska i kalendarska računanja, a da je „pravi“ vigzemalni sitem korišćen u svakodnevnom životu [6].

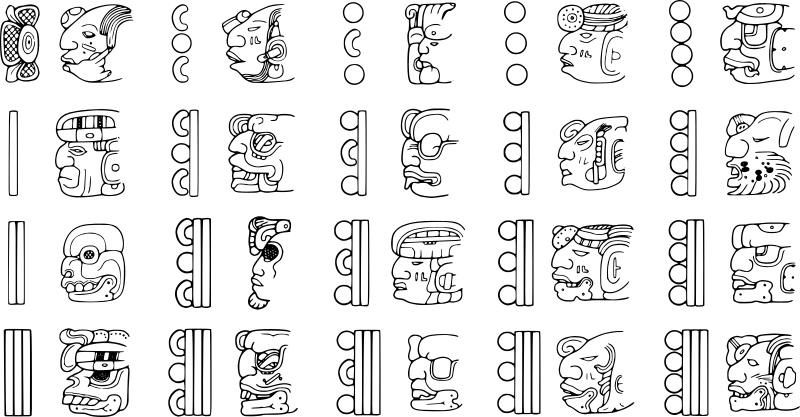
Cifre koje su Maje koristile bile su podložne menjanju isto koliko i pismo Maja. Tako se u nekim tekstovima može videti promena orijentacije cifara, različito stilizovanje (posebno cifre 0), kao i spajanje s logogramima. Jedan primer originalnog teksta sa ciframa dat je na slici 4. Takođe, Maje su imale alternativne zapise za brojeve do dvadeset u obliku glava bogova (slika 3). Tako bi s glavom boga vetra bio predstavljen broj 3, s glavom boga Meseca broj 4, s glavom boga smrti broj 10 i tako dalje... Ovakvi zapisi oslikavaju numerološka verovanja Maja.

Astronomija i kalendar

Za Maje, astronomski fenomeni su bili od izuzetne važnosti, zato što su religijski rituali izvođeni u skladu s tim fenomenima. Stoga ne čudi činjenica da su Maje imale razvijen sistem računanja vremena. Maje su vreme računale uz pomoć dva kalendara: ritualnog i solarnog kalendara.

Solarni kalendar Maja, Haab, se sastoji od 365 dana raspoređenih u 19 meseci⁷ po 20 dana i perioda⁸ od prestalih 5 dana. Dani u okviru svakog meseca su numerisani od nule, dok sami meseci nisu bili numerisani već su imali posebna imena (ta imena su Pop, Uo, Zip, Zotez, Tzac, Xul, Yaxkin, Mol, Ch’en, Yax, Zac, Ceh, Mac, Kankin, Muan, Pax, Kayab, Cumku i pomenuti period od 5 dana Wayeb).

Ritualni kalendar, Tzolkin, se sastoji od 260 dana koji su numerisani uz pomoć perioda od 13 dana i perioda od 20 dana. Period od 13 dana bi se označavao sa ciframa (počinjući od jedinice), dok bi se period od 20 dana označavao imenima (ta imena su: Imix, Ik, Akbal, Kan, Chicchan, Cimi, Manik, Lamat, Muluc, Oc, Chuen, Eb, Ben, Ix, Men, Cib, Caban, Etznab, Cauc i Ahau). Za razliku od solarnog kalendara Maja, u kom su dani organizovani u mesece, a meseci u godinu, u Tzolkin-u, opisane numeracije od 13 i 20 dana bi se svakodnevno pomerale nezavisno jedna od druge (slika 5). Zato bi posle dana 1 Imix (prvi dan Tzolkin-a), usledio 2 Ik, pa 3 Kan, itd... Za sada ne postoji opšte prihvaćena teorija zašto su Maje koristile kalendar od 260 dana.

Poznato je da su i ostale mezoameričke civilizacije koristile dva kalendara (jedan od 365 dana i drugi od 260 dana). Ta činjenica ide u prilog teoriji po kojoj su Maje preuzele i kalendare od Olmeka.

Sa opisanim kalendarima postoji jedan problem. Naime, samo uz pomoć Haab-a, odnosno Tzolkin-a, nije moguće razlikovati dva datuma koji se razlikuju za 365, odnosno 260, dana. Drugim rečima, datumi u opisanim kalendarima ne podrazumevaju i oznaku za kalendarsku godinu. Taj problem Maje su rešile korišćenjem oba kalendara istovremeno. Dva opisana kalendara definišu ciklus od NZD(260,365)=18980 dana što iznosi 52 (solarne) godine. Ako se svakom danu dodele oba datuma, tada će tokom 52 godine dani imati jedinstvene datume, što je često bilo dovoljno.

Za apsolutno merenje vremena, Maje su koristile treći kalendarski sistem (na engleskom nazvan Long Count). U ovom sistemu, datum bi se jednostavno označavao brojem proteklih dana od dana za kog su Maje smatrale da predstavlja stvaranje sveta. Različiti istoričari različito procenjuju tačan datum ovog dograđaja. Po [7] Maje su za ovaj dan uzimale 12. avgust 3113. p.n.e, dok je u [2] procenjen na 5. septembar 3114. p.n.e. Kako su Maje koristile modifikovan vigezimalni sistem, u kojem treća cifra predstavlja umnoške broja 360, u ovom apsolutnom sistemu se isticao period od 360 dana kojeg su Maje nazivale tun. Dvadeset tun-ova činilo je jedan katun, dok je dvadeset katun-ova činilo jedan baktun, itd... Trinaesti baktun se završio decembra 2012. godine⁹.

Primetimo da svakom od pomenutih vremenskih intervala odgovara po jedna cifra u brojevnom sistemu Maja¹⁰. To je omogućavalo jednostavno računanje sa datumima izraženim u Long Count-u.

Geometrija

U četiri sačuvane knjige iz perioda Maja nema nikakvih informacija koje bi nam nešto rekle o geometrijskim znanjima koje su Maje posedovale. Međutim, analizom hramova, kuća, opservatorija, puteva kao i čitavih gradova koji su sačuvani do današnjih dana u džunglama Mezoamerike, postaje jasno da su Maje morale posedovati osnovna znanja iz geometrije (u originalnom smislu te reči). Maje su s neverovatnom preciznošću konstruisale prave uglove i paralelne linije prilikom gradnje pomenutih objekata.

Takođe, u slikama (u kodeksima, na grnčariji i na zidovima) koje su sačuvane do danas, moguće je primeti upotrebu lenjira i šestara.

Detaljnije analize geometrije Maja, mogu se pronaći u radu [11] ili u disertaciji¹¹ [8].

1. Brojevni sistem s bazom 20. Reč vigezimalni vodi poreklo od latinske reči za broj dvadeset – vicesimus. ↩
2. Zainteresovan čitalac može pronaći detaljnu istoriju dešifrovanja pisma Maja u knjizi [4]. ↩
3. Logogram je simbol koji predstavlja reč. ↩
4. Silabogram je simbol koji predstavlja slog. ↩
5. Vigzemalni brojevni sistem su koristila i neka plemena Severne Amerike. ↩
6. Civilizacija Olmeka jeste prva Mezoamerička civilizacja. Ova civilizacija doživela je svoj vrhunac u IX veku pre nove ere, na jugozapadnoj obali Meksičkog zaliva, da bi do III veka pre nove ere nestala. Kultura Olmeka značajno je uticiala na sve ostale Mezomaeričke kulture. ↩
7. Iako ovde koristimo izraz mesec, napomenimo da ovi periodi nisu imali nikakve veze s Mesecom. ↩
8. Maje su ovaj period, Wayeb, smatrale nesrećnim. Tokom ovog meseca Maje su prekidale teške poslove. ↩
9. Ova činjenica je izvor tvrdnji o smaku sveta koje su bile popularne tokom 2012. godine. ↩
10. Prirodno se postavlja pitanje, da li je vigezimalni sistem modifikovan tako da bi se slagao s Long Count-om, ili je Long Count kreiran tako da se „lepo slaže“ sa brojevnim sistemom Maja. Za sada nema definitivnih arheoloških odgovora. ↩
11. Ova disertacija je posebno zanimljiva zbog toga što se u njoj iznose hipoteze po kojima su značajne građevine u skladu s nekim neobičnim proprcijama (kao što je između ostalog i zlatni presek). ↩

Literatura

1. Anderson, W. F. Arithmetic in maya numerals. American Antiquity 36 (1971).
2. Blackburn, B., and Holford-Strevens, L. The Oxford Companion to the Year. Oxford University Press, Oxford, 1999.
3. Closs, M. P. The Mathematical Notation of the Ancient Maya. In Native American Mathematics. University of Texas Press, Austin, 1986.
4. Coe, M. D. Breaking the Maya Code. Thames & Hudson, London, 2012.
5. Coe, M. D., and Stone, M. V. Reading The Maya Glyphs. Thames & Hudson, London, 2005.
6. Ifrah, G. A universal history of numbers : From prehistory to the invention of the computer. Oxford University Press, London, 1998.
7. O’Connor, J. J., and Robertson, E. F. Mayan mathematics, 2000.
8. Powell, C. The Shapes of Sacred Space : A Proposed System of Geometry Used to Lay Out and Design Maya Art and Architecture and Some Implications Concerning Maya Cosmology. PhD thesis, University of Texas, Austin, 2010.
9. Seidenberg, A. The Zero in the Mayan Numerical Notation. In Native American Mathematics. University of Texas Press, Austin, 1986.
10. Stone, A., and Zender, M. Reading Maya Art. Thames & Hudson, London, 2011.
11. Vinette, F. In Search of Mesoamerican Geometry. In Native American Mathematics. University of Texas Press, Austin, 1986.