Žulijev i Mandelbrotov skup

Francuski matematičar Gaston Žulija¹ je 1918. godine objavio rad Mémoire sur l'itération des fonctions rationnelles u kome je proučio iteracije kompleksnih racionalnih funkcija. Iako Žulija nije bio prvi matematičar koji se bavio iteracijama racionalnih funkcija, Žulija je ovim radom sistematizovao dotadašnje znanje, i time zasnovao novu matematičku oblast, kasnije nazvanu kompleksna dinamika. Važnost Žulijevog doprinosa je prepoznata u matematičkim krugovima, i Žulija je nagrađen nagradom Francuske akademije nauke, što je doprinelo popularnosti kompleksne dinamike među matematičarima.

Ipak, početna zainteresovanost matematičara za kompleksnu dinamiku je polako jenjavala tokom narednih godina, da bi do tridesetih godina prošlog veka, potpuno nestala. Tek će pedeset godina kasnije, Žulijev učenik, Benoa Mandelbrot² nastaviti tamo gde je njegov učitelj stao.

Mandelbrot je uspeo da zainteresuje naučnu zajednicu za Žulijev skup, i za skup koji će kasnije biti poznat pod imenom Mandelbrotov skup. Zanimljivi oblici navedenih skupova doprineli su njihovoj, sada već velikoj, popularnosti u široj javnosti.

U nastavku ovog teksta biće opisana osnovna svojstva Mandelbrotovog i Žulijevih skupova, kao i nekoliko algoritama za njihovo crtanje. Sadržaj teksta je naveden u narednoj listi. Za opširniji pregled istorije kompleksne dinamike čitaoce upućujemo na [1].

Žulijev skup

Neka je $f:ℂ\to ℂ$ funkcija određena polinomom sa kompleksnim koeficijentima, tj. $f(z)=a_n{z}^n+a_{n-1}{z}^{n-1}+\dots +a_0$. Pitanje koje nas interesuje, ili je barem interesovalo Žuliju, glasi: kakve su osobine funkcije $f^k$ kada $k$ teži beskonačnosti (gde $f^k$ označava kompoziciju $f\circ \dots \circ f$ sa $k$ članova). Za proučavanje ovakvih iteracija, od izuzetne koristi će nam biti pojmovi koje ćemo u nastavku definisati:

Neka je $z_0$ proizvoljna tačka u kompleksnoj ravni, i neka je $f:ℂ\to ℂ$ holomorfna funkcija (ne obavezno polinomska). Orbita tačke $z_0$, u oznaci ${𝒪}_f\left(z_0\right)$, je niz ${(f^k(z_0))}_{k\in \mathbb{N}}$. Tačka $z_0$ je fiksna tačka preslikavanja $f$ ako je $f\left(z_0\right)=z_0$. Ako je $f^p\left(z_0\right)=z_0$ za neko prirodno $p$, tada tačku $z_0$ nazivamo periodičnom tačkom. Najmanje $p$ za koje važi jednakost $f^p\left(z_0\right)=z_0$ je period tačke $z_0$. Jasno, periodična tačka $z_0$ je fiksna ako i samo ako je njen period $1$. Orbitu periodične tačke nazivamo cikl. Ako je $z_0$ periodična tačka sa periodom $p$, izvod $\left(f^p\right)\prime \left(z_0\right)=\lambda$ nazivamo multiplikator, a tačku $z_0$ nazivamo privlačeća, neutralna ili odbijajuća u zavisnosti od toga da li je $0\le |\lambda |<1$, $|\lambda |=1$ ili $|\lambda |>1$. Primetimo da multiplikator ne zavisi od izbora tačke cikla, jer po formuli za izvod kompozicije funkcije važi $\left(f^p\right)\prime \left(z_0\right)={\prod }_{i=0}^{p-1}f\prime (z_{0+i})$. Prema tome za sam cikl možemo da kažemo da je privlačeći, neutralan ili odbijajući u zavisnosti od odgovarajućeg multiplikatora. Ako tačka $z_0$ nije sama periodična, ali se u njenoj orbiti nalazi periodična tačka, za tačku $z_0$ kažemo da je predperiodična.

Izrazi, privlačeća, odnosno odbijajuća, tačka, ukazuju na to kako se ponaša okolina tih tačaka pri iteracijama funkcije $f$. Tačnije, važe naredne dve teoreme:

Teorema 1. Neka je $z_0$ privlačeća fiksna tačka holomorfne funkcije $f$. Tada postoji disk $D$ sa centrom u $z_0$ sa sledećom osobinom: ako $z\in D$ tada $f^k\left(z\right)\to z_0$ kad $k\to \infty$.

Teorema 2. Neka je $z_0$ odbijajuća fiksna tačka holomorfne funkcije $f$. Tada postoji disk $D$ sa centrom u $z_0$ sa sledećom osobinom: ako $z\in D$ i $z\ne z_0$ tada postoji prirodan broj $k$ takav da je $f^k\left(z\right)\notin D$.

Dokaz teoreme 1. Kako je $|f\prime (z_0)|<1$ sledi da postoje $\delta >0$ i $\mu <1$ takvi da za svako $z$ za koje je $|z-z_0|<\delta$ važi $$\left|\frac{f(z)-f(z_0)}{z-z_0}\right|<\mu .$$ Ako za disk $D$ uzmemo disk centriran u $z_0$ sa poluprečnikom $\delta$, tada će navedena jednakost biti ispunjena za sve tačke $z$ iz tog diska. Pritom važi $|f(z)-z_0|=|f(z)-f(z_0)|<\mu |z-z_0|$. Ponavljajući navedeni argument $k$ puta, zaključujemo da je $|f^k(z)-z_0|<{\mu }^k|z-z_0|$. Kako je $\mu <1$, sledi da $|f^k(z)-z_0|\to 0$ kad $k\to \infty$, što je i trebalo dokazati. □

Dokaz teoreme 2 je analogan.

Vratimo se sada na pitanje sa početka ovog poglavlja: kakve su osobine polinomske funkcije $f^k$ kada $k$ teži beskonačnosti. Ako je $f\left(z\right)=az+b$, tada $f$ predstavlja direktnu konformnu afinu transformaciju kompleksne ravni. Ponašanje ovakvih transformacija je u potpunosti poznato, pa ih u ovom tekstu nećemo proučavati. Ako je funkcija $f$ polinom stepena $n\ge 2$, tada je naredno tvrđenje izuzetno korisno prilikom ispitivanja iteracija funkcije $f$.

Teorema 3. Ako je $f\left(z\right)=a_n{z}^n+a_{n-1}{z}^{n-1}+\dots +a_0$, gde je $a_n\ne 0$ i $n\ge 2$, tada postoji realan broj $R\ge 1$ takav da $|z|>R$ povlači $f^k\left(z\right)\to \infty$.

Dokaz: Neka je $\gamma >1$ proizvoljno, i $$R=max\{1,2\frac{\left|a_{n-1}\right|+\cdots +\left|a_0\right|}{|a_n|},{\left(\frac{2\gamma }{|a_n|}\right)}^{\frac{1}{n-1}}\}.$$

Neka je $|z|>R$. Tada, $$\begin{array}{cc}\hfill |f\left(z\right)|& \ge |a_n||z{|}^n-(|a_{n-1}||z{|}^{n-1}+\dots +|a_1||z|+|a_0|)\hfill \\ \hfill & \ge |a_n||z{|}^n-|z{|}^{n-1}(|a_{n-1}|+\dots +|a_1|+|a_0|)\hfill \\ \hfill & =|z{|}^n(|a_n|-\frac{|a_{n-1}|+\dots +|a_1|+|a_0|}{|z|})\hfill \\ \hfill & >|z{|}^n\frac{1}{2}|a_n|=\frac{1}{2}|z||a_n||z{|}^{n-1}\hfill \\ \hfill & >|z|\gamma ,\hfill \end{array}$$ pa je i $|f\left(z\right)|>R$. Indukcijom sledi $\left|f^k\left(z\right)\right|>{\gamma }^k\left|z\right|>{\gamma }^{k}R$. Odavde sledi da $f^k\left(z\right)\to \infty$ kada $k\to \infty$. □

Primetimo da iz gornjeg tvrđenja sledi da za svaku tačku $z\in ℂ$ postoje dve međusobno isključujuće mogućnosti: ili je orbita tačke $z$ ograničena ili $f^k(z)\to \infty$. Zato uvodimo naredne definicije. Ispunjen Žulijev skup ${𝒦}_f$ funkcije $f$ je skup svih tačaka kompleksne ravni čije orbite ostaju ograničene prilikom iteracije funkcije $f$. Žulijev skup ${𝒥}_f$ funkcije $f$ definišemo kao granicu ispunjenog Žulijevog skupa, tj. ${𝒥}_f=\partial {𝒦}_f$. Fatuov³ skup ${ℱ}_f$ funkcije $f$ definišimo kao $ℂ\backslash {𝒥}_f$. Iz definicije Žulijevog skupa sledi da tačka $z$ pripada Žulijevom skupu ako i samo ako u svakoj njenoj okolini postoje kompleksni brojevi $w_1$ i $w_2$ takvi da $f^k(w_1)\to \infty$ i $f^k(w_2)\to ̸\infty$.

Primer 1. Utvrdimo za početak Žulijev skup funkcije $f(z)=z^2$. Prelaskom na polarne koordinate, vidimo da je $f(z)=r^2{e}^{i2\theta }$, gde je $r=\left|z\right|$ a $\theta =arg\left(z\right)$, pa je $f^k(z)=r^{2^k}{e}^{i{2}^k\theta }$. Kako je $\left|r^{2^k}{e}^{i{2}^k\theta }\right|=r^{2^k}$, lako možemo zaključiti šta se dešava sa proizvoljnom tačkom prilikom iteracija funkcije $f$. Ako je $r<1$ tada $r^{2^k}\to 0$, pa $f^k(z)\to 0$ kad $k\to \infty$. Slično, ako je $r>1$ tada $f^k(z)\to \infty$ kad $k\to \infty$. Konačno ako je $r=1$ tada se sve tačke orbite ${𝒪}_f\left(z\right)$ nalaze na jediničnoj kružnici. Iz svega navedenog sledi da je ${𝒦}_f$ funkcije $f(z)=z^2$ jedinični disk centriran u nuli, a ${𝒥}_f$ jedinična kružnica centrirana u nuli. ▲

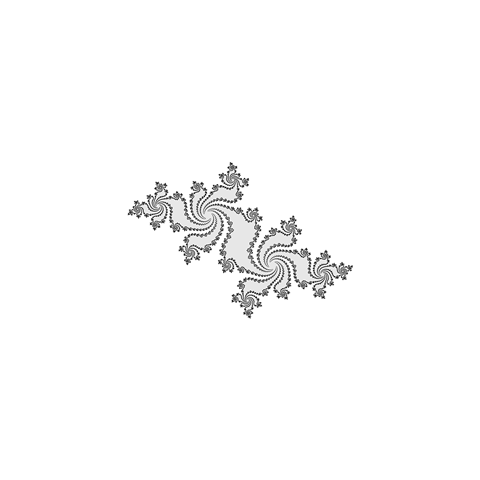
Do istog zaključka dolazimo ako posmatramo funkciju $f(z)=z^n$ za bilo koje $n\ge 2$. Kao što ćemo videti, za (skoro) sve ostale polinomske funkcije, odgovarajući Žulijevi skupovi će biti mnogo komplikovaniji objekti. Primer jednog takvog skupa je prikazan na figuri 1.

Naredna teorema opisuje osnovne osobine definisanih skupova.

Teorema 4. Neka su $𝒦$, $𝒥$ i $ℱ$ ispunjen Žulijev skup, Žulijev skup i Fatuov skup kompleksne polinomske funkcije $f$. Tada važe naredna tvrđenja.

1. $𝒦$ i $𝒥$ su kompaktni skupovi i važi $𝒥\subset 𝒦$.
2. $𝒦$ i $𝒥$ su neprazni skupovi.
3. Skup $𝒥$ ima prazan interior.
4. Skup $𝒥$ je invarijantan za $f$ i $f^{-1}$.
5. Za svako prirodno $m$ važi ${𝒥}_{f^m}=𝒥$.

Dokaz:

1. Ako $z\notin 𝒦$ tada $f^k(z)\to \infty$, pa sledi da je $f^m(z)>R$ za neko prirodno $m$, gde je $R$ poluprečnik određen u teoremi 3. Zbog neprekidnosti funkcije $f^m$ sledi da postoji dovoljno mali disk $D_{\epsilon }(z)$ takav da za svako $w\in D_{\epsilon }(z)$ važi $f^m(w)>R$, tj. $f^k(w)\to \infty$. Po definiciji ispunjenog Žulijevog skupa sledi da je $D_{\epsilon }(z)\cap 𝒦=\varnothing$, pa zaključujemo da je skup $𝒦$ zatvoren. Samim tim važi da mu pripada njegova granica $𝒥$ i da je i ona zatvorena. Iz teoreme 3 sledi i da su skupovi $𝒦$ i $𝒥$ ograničeni, a kako su i zatvoreni, sledi da su kompaktni.
2. Jednačina $f(z)=z$ ima barem jedno rešenje, neka je to $z_0$, iz čega sledi da $z_0\in 𝒦$, pa je skup $𝒦$ neprazan. Neka je sada $z_1\notin {𝒦}_f$ (postojanje ovakvog broja $z_1$ sledi iz teoreme 3). Tada će za neko realno $0\le \lambda \le 1$ tačka $\lambda z_0+(\lambda -1)z_1$ pripadati granici skupa $𝒦$. Dakle i $𝒥$ je neprazan skup.
3. Skup $𝒥$ kao granica zatvorenog skupa $𝒦$ mora imati prazan interior.
4. Neka $z\in 𝒥$. Tada $f^k(z)\to ̸\mathrm{\infty },$, ali u svakoj okolini tačke $z$ postoji tačka $w$ takva da $f^k(w)\to \infty$. Odavde sledi da $f^k(f(z))\to ̸\mathrm{\infty }$ i $f^k(f(w))\to \infty$. Zbog neprekidnosti funkcije $f$, tačke $f(z)$ i $f(w)$ mogu biti proizvoljno bliske, zaključujemo da $f(z)\in 𝒥$. Dakle $f\left[𝒥\right]\subset 𝒥$, iz čega sledi da $𝒥\subset f^{-1}\left[𝒥\right]$. Ako je $f(z\prime )=z$ tada za svako $w$ iz dovoljno male okoline tačke $z$, postoji $w\prime$ u okolini tačke $z\prime$ takvo da je $f\left(w\prime \right)=w$. Odavde sledi da $f^k\left(f\left(z^{\mathrm{\prime }}\right)\right)\to ̸\mathrm{\infty }$ i $f^k\left(f\left(w\prime \right)\right)\to \infty$. Dakle $f^{-1}\left[𝒥\right]\subset 𝒥$ i $𝒥\subset f\left[𝒥\right]$.
5. Iz teoreme 3 sledi da $f^k(z)\to \infty$ ako i samo ako $(f^m{)}^k(z)=f^{mk}(z)\to \infty$. Dakle funkcije $f$ i $f^m$ imaju iste ispunjene Žulijeve skupove, pa imaju iste i Žulijeve skupove.

□

Različite funkcije mogu veoma „slično“ delovati na kompleksnu ravan. Bilo bi veoma korisno kada bismo mogli da proučimo svojstva svih polinomskih funkcija, proučavajući svojstva neke manje klase funkcija. Smisao naredne definicije je upravo preciziranje pojma sličnosti među funkcijama.

Neka su $f$ i $g$ dve kompleksne funkcije kompleksne promenljive. Ako postoji bijekcija $\varphi :ℂ\to ℂ$ takva da važi $\varphi \circ f=g\circ \varphi$, za funkcije $f$ i $g$ reći ćemo da su konjugovane funkcijom $\varphi$.

Što više finih osobina poseduje funkcija $\varphi$,, poput neprekidnosti ili holomorfnosti, to će funkcije $f$ i $g$ biti sličnije. Tako na primer, prilikom svake konjugacije, periodične tačke se slikaju u periodične tačke, pri čemu se period čuva, a ako je $\varphi$ konformno preslikavanje, tada se multiplikatori čuvaju. Ako su dve funkcije konjugovane funkcijom oblika $\varphi (z)=az+b$, njihovi Žulijevi skupovi će biti slični u geometrijskom smislu. Ovo sledi iz činjenice da funkcije oblika $\varphi (z)=az+b$ geometrijski predstavljaju kombinaciju rotacije, homotetije i translacije.

Primer 2. Uz pomoć pojma konjugacije možemo odrediti Žulijev skup funkcije $g(z)=z^2-2$. Neka je $f(z)=z^2$ i neka je funkcija⁴ $\varphi (z)=z+z^{-1}$ definisana na komplementu jediničnog diska ${𝔻}^{\complement }=\left\{z\right|\left|z\right|>1\}$. Lako se proverava da je funkcija $\varphi$ injekcija na svom domenu. Naime, ako je $\varphi \left(z\right)=\varphi \left(w\right)$ tada, iz definicije funkcije $\varphi$, sledi da je $zw=1$. Odavde sledi da je $\left|z\right|\left|w\right|=1$, pa najviše jedan od brojeva $z$ i $w$ može pripadati skupu ${𝔻}^{\complement }$. Dokažimo da funkcija $\varphi$ slika domen ${𝔻}^{\complement }$ na skup $ℂ\backslash [-2,2]$. Rešavajući jednačinu $w=\varphi (z)$ po $z$, dobijamo da je inverzna funkcija funkcije $\varphi$ višeznačna funkcija data sa $z_{\pm }=\frac{1}{2}(w\pm \sqrt{w^2-4})$. Kako je $z_{+}{z}_{-}=1$, sledi da najviše jedan od brojeva $z_{+}$ i $z_{-}$ može pripadati skupu ${𝔻}^{\complement }$. Ako se $z_{+}$ i $z_{-}$ nalaze na jediničnoj kružnici, tada je $\varphi \left(z_{+}\right)=\varphi \left(z_{-}\right)=2cos\left(arg\left(z\right)\right)\in [-2,2]$. Prema tome $\varphi$ je bijekcija između skupova ${𝔻}^{\complement }$ i $ℂ\backslash [-2,2]$.

Direktnim računom se proverava da je $\varphi \circ f=g\circ \varphi$ odnosno $\varphi \circ f\circ {\varphi }^{-1}=g$. Prema tome važi $g^n=\varphi \circ f^n\circ {\varphi }^{-1}$. Neka je sad $z\in ℂ\backslash [-2,2]$ proizvoljna tačka. Tada je $g^n(z)=\varphi \left(f^n\left({\varphi }^{-1}\left(z\right)\right)\right)$. Kako ${\varphi }^{-1}\left(z\right)$ pripada skupu ${𝔻}^{\complement }$, iz primera 1 sledi da $f^n\left({\varphi }^{-1}\left(z\right)\right)\to \infty$ kad $n\to \infty$. Prema tome i $g^n(z)=\varphi \left(f^n\left({\varphi }^{-1}\left(z\right)\right)\right)\to \infty$ kad $n\to \infty$. Slično se dokazuje da ako $z\in [-2,2]$ tada $g^n\left(z\right)\in [-2,2]$. Prema tome, (ispunjen) Žulijev skup funkcije je segment $[-2,2]$. ▲

Mandelbrotov skup

U ovom poglavlju, posvetićemo se polinomskim funkcijama oblika $f_c(z)=z^2+c$ (i oznaku $f_c(z)$ ćemo koristiti isključivo za $z^2+c$). Naredna teorema nam govori da je svaka polinomska funkcija stepena $2$ afino konjugovana jednoj funkciji oblika $f_c(z)=z^2+c$. Prema tome, za proučavanje Žulijevih skupova svih polinomskih funkcija stepena dva, dovoljno je posmatrati funkcije oblika $f_c$.

Teorema 5. Neka je $g(z)=\alpha z^2+\beta z+\gamma$. Tada $\varphi (z)=\alpha z+\beta /2$ ostvaruje konjugaciju između $g$ i $f_c$ , tj. $\phi \circ g=f_c\circ \phi$, gde je $$c=\frac{1}{2}(2\beta -{\beta }^2+4\alpha \gamma ).$$

Takođe, ako su $f_{c_1}$ i $f_{c_2}$ dve afino konjugovane funkcije, tada je $c_1=c_2$.

Dokaz: Navedena teorema se direktno dokazuje. □

Definišimo sada Mandelbrotov skup.

Mandelbrotov skup $ℳ$ je skup svih tačaka kompleksne ravni za koje je ispunjen Žulijev skup funkcije $f_c$ povezan.

Da bismo odredili oblik ispunjenog Žulijevog skupa, a samim tim i odredili da li je on povezan, primenićemo sledeću ideju: Neka je $D$ disk sa centrom u nuli, takav da je ${𝒦}_{f_c}\subset D$, i neka je $R$ poluprečnik ovog diska. Posmatrajmo niz indirektnih slika $D_k=f_c^{-k}\left[D\right]$. U skupu $D_k$ nalaze se se svi kompleksni brojevi $z$ takvi da je $|f^k(z)|\le R$. Prema tome ${𝒦}_{f_c}\subset D_k$ za svako prirodno $k$. Kako $k$ raste, tako raste i „broj“ tačaka kompleksne ravni $z$ za koje je $|f^k(z)|>R$. Dakle skup $D_k$ se smanjuje, a kako ${𝒦}_{f_c}\subset D_k$ za svako prirodno $k$, za očekivati je da će $D_k$ „težiti“ ispunjenom Žulijevom skupu ${𝒦}_{f_c}$. Na ovaj način ćemo odrediti skup ${𝒦}_{f_c}$. Naredne definicije i leme pomoći će nam u formalizaciji navedene ideje.

Neprekidnu, zatvorenu, prostu, krivu u kompleksnoj ravni nazivamo petlja. Po poznatoj Žordanovoj teoremi, svaka petlja $C$ određuje u ravni dva povezana skupa: jedan neograničen i drugi ograničen. Neograničen skup nazivamo spoljašnjost petlje $C$, a ograničen skup nazivamo unutrašnjost petlje $C$. Uniju dve petlje koje imaju tačno jednu zajedničku tačku, nazivamo lemniskata.

Lema 1. Neka je $C$ petlja u kompleksnoj ravni.

1. Ako $c$ pripada unutrašnjosti petlje $C$, tada je $f_c^{-1}\left[C\right]$ petlja čija je unutrašnjost inverzna slika unutrašnjosti petlje $C$.
2. Ako $c$ pripada petlji $C$, tada je $f_c^{-1}\left[C\right]$ lemniskata, čija je unutrašnjost inverzna slika unutrašnjosti petlje $C$.
3. Ako $c$ pripada spoljašnjosti petlje $C$, tada je $f_c^{-1}\left[C\right]$ unija dve petlje, a unija njihovih unutrašnjosti je inverzna slika unutrašnjosti petlje $C$.

Dokaz: Primetimo da su $f_c^{-1}(z)=\pm \sqrt{z-c}$ i $(f_c^{-1})\prime (z)=\pm \frac{1}{2}(z-c{)}^{-\frac{1}{2}}$ konačni i različiti od nule za $z\ne c$. Prema tome, ako $C$ ne sadrži tačku $c$, tada je $f_c^{-1}$ lokalni difeomorfizam u okolini krive $C$. Označimo sa $+f_c^{-1}$ i $-f_c^{-1}$ dve grane funkcije $f_c^{-1}$. Razlikujemo naredna tri slučaja.

1. Tačka $c$ pripada unutrašnjosti petlje $C$: Neka je $w$ fiksirana tačka na petlji $C$. Ako tačka $z$ od tačke $w$ krene da „šeta“ po petlji $C$, tada će, zbog neprekidnosti funkcije $+f_c^{-1}$ u okolini petlje $C$, tačka $+f_c^{-1}\left(z\right)$ početi da opisuje krivu. Kada $z$ prvi put stigne do $w$, tačka $+f_c^{-1}\left(z\right)$ će stići do tačke $-f_c^{-1}\left(w\right)$, a kada $z$ drugi put stigne do $w$, tačka $+f_c^{-1}\left(z\right)$ će stići do tačke $+f_c^{-1}\left(w\right)$ zatvarajući krivu $f_c^{-1}(C)$. Kako je u okolini krive $C$ funkcija $+f_c^{-1}$ lokalni difeomorfizam, kriva $f_c^{-1}\left[C\right]$ ne može imati samopreseka. Pošto polinom $f_c$ preslikava tačke iz skupa $f_c^{-1}\left[C\right]$, i samo te tačke, na $C$, $f_c$ mora preslikavati unutrašnjost i spoljašnjost petlje $f_c^{-1}\left[C\right]$ na unutrašnjost i spoljašnjost petlje $C$. Dakle $f_c^{-1}$ slika unutrašnjost petlje $C$ na unutrašnjost petlje $f_c^{-1}\left[C\right]$.
2. Tačka $c$ pripada petlji $C$: U ovom slučaju, krive, koje opisuju tačke $+f_c^{-1}\left(z\right)$ i $-f_c^{-1}\left(z\right)$, će se preseći kada $z$ „stigne“ do $c$. Zbog toga je skup $f_c^{-1}\left[C\right]$ lemniskata.
3. Tačka $c$ pripada spoljašnjosti petlje $C$: U ovom slučaju $+f_c^{-1}\left(z\right)$ može proći samo kroz tačku $+f_c^{-1}\left(w\right)$, a $-f_c^{-1}\left(z\right)$ može proći samo kroz tačku $-f_c^{-1}\left(w\right)$. Odavde sledi da se $f_c^{-1}\left[C\right]$ sastoji od dve petlje.

□

Lema 2. Ako je $F_n$ niz kompaktnih povezanih podskupova Hausdorfovog⁵ prostora⁶, tada je $F={\bigcap }_{n=1}^{\infty }{F}_n$ povezan skup.

Dokaz: Pretpostavimo suprotno. Tada postoje disjunktni otvoreni skupovi $A$ i $B$ takvi da je $F\subseteq A\cup B$ i $F$ sadrži tačke i iz skupa $A$ i iz skupa $B$. Kako je svaki od skupova $F_n$ povezan, i sadrži tačke i iz $A$ i iz $B$, sledi da je svaki od skupova $\partial A\cap F_n$ neprazan. Štaviše, $\partial A\cap F_n$ je opadajući niz kompaktnih skupova, pa po Kantorovoj⁷ lemi⁸, presek ${\bigcap }_{n=1}^{\infty }\partial A\cap F_n$ je neprazan. Kontradikcija. □

Teorema 6. Važi $$\mathcal{M}=\{c\in \mathbb{C}\hspace{0.25em} |\hspace{0.25em} f_c^k(0)\to ̸\mathrm{\infty },\hspace{0.25em} (k\to \mathrm{\infty })\}\mathrm{.}$$

Dokaz: Neka je $C$ kružnica sa centrom u nuli, sa poluprečnikom $R$ koji je određen iz teoreme 3 za funkciju $f_c$. Ako je orbita ${𝒪}_{f_c}\left(0\right)$ ograničena, tada je tačka $c=f_c(0)$ u unutrašnjosti petlje $C$, pa po lemi 1 sledi da je $f_c^{-1}\left[C\right]$ petlja u unutrašnjosti petlje $C$. Takođe, $f_c^2(0)$ pripada unutrašnjosti petlje $C$, pa po istoj lemi, sledi da $f^{-1}(f_c^2(0))=c$ pripada unutrašnjosti petlje $f_c^{-1}\left[C\right]$. Primenjujući ponovo lemu 1, zaključujemo da je $f_c^{-2}\left[C\right]$ petlja sadržana u unutrašnjosti petlje $f_c^{-1}\left[C\right]$. Na ovaj način, dobijamo niz petlji $f_c^{-n}\left[C\right]$ tako da svaka petlja u svojoj unutrašnjosti sadrži narednu. Neka je $P={\bigcap }_{k=1}^{\infty }{D}_k$ gde je $D_k$ adherencija unutrašnjosti petlje $f_c^{-n}\left[C\right]$. Tačka $z$ pripada skupu $ℂ\backslash P$ ako i samo ako za neko prirodno $k$ važi $|f_c^k(z)|>R$, tj. ako i samo ako $f_c^k(z)\to \infty$. Dakle $P$ je ispunjen Žulijev skup funkcije $f_c$. Kako je skup $P$ presek monotonog niza povezanih kompaktnih skupova, iz leme 2 sledi da je i sam povezan.

Ako neka tačka $f_c^p\left(0\right)$ orbite ${𝒪}_{f_c}\left(0\right)$ pripada kružnici $C$, tada je skup $f_c^{-p}\left[C\right]$, po prethodnoj lemi, lemniskata. Dalje, skup $f_c^{-(p+1)}\left[C\right]$ je unija dve lemniskate sa disjunktnim unutrašnjostima, skup $f_c^{-(p+2)}\left[C\right]$ je unija četiri lemniskate sa disjunktnim unutrašnjostima, itd… Kako u prethodnom delu dokaza, zaključujemo da je ${𝒦}_{f_c}={\bigcap }_{n=1}^{\infty }{f}_c^{-n}\left[C\right]$. Pritom se skup ${\bigcap }_{n=1}^{p+m}{f}_c^{-n}\left[C\right]$ sastoji od $2^{m-1}$ lemniskate sa disjunktnim unutrašnjostima, pa Žulijev skup u ovom slučaju nije povezan. Zapravo, u ovom slučaju Žulijev skup je homeomorfan Kantorovom skupu⁹.

Ako orbita ${𝒪}_{f_c}\left(0\right)$ nije ograničena, tada postoji neko najmanje prirodno $p$ za koje važi važi $|f_c^p(z)|>R$. Tada se uzastupnom primenom leme 1 dobija da se skup $f_c^{-(p+k)}\left[C\right]$ sastoji od $2^{k-1}$ petlji sa disjuntktnim unutrašnjostima. I u ovom slučaju Žulijev skup je homeomorfan Kantorovom skupu. □

Kao što vidimo, u navedenom dokazu je iskorišćen položaj kritične tačke, odnosno tačke $z$ za koju je $f_c\prime (z)=0$. Kod polinoma stepena $2$, postoji tačno jedna kritična tačka (za polinome oblika $z^2+c$ to je baš $z=0$). Polinomi stepena većeg od dva mogu imati i više kritičnih tačaka. Analogno se može dokazati da je Žulijev skup tih polinoma povezan ako i samo ako mu pripadaju sve kritične tačke. U slučaju da barem jedna od kritičnih tačaka ne pripada Žulijevom skupu, tada se on sastoji od neprebrojivo mnogo povezanih komponenti, pri čemu te komponente ne moraju biti jednočlani skupovi. Kada se sve kritične tačke nalaze van Žulijevog skupa, tada je svaka od komponenti povezanosti jednočlan skup, i Žulijev skup je homeomorfan Kantorovom skupu.

Vratimo se na polinome stepena $2$. Naredna teorema je poboljšanje rezultata teoreme 3:

Teorema 7. Neka je $f_c(z)=z^n+c$, $n\ge 2$, gde je $c$ proizvoljna tačka kompleksne ravni. Tada $f_c^k\left(0\right)\to ̸\mathrm{\infty }$ kad $l\to \infty$ ako i samo ako je $|f_c^k\left(0\right)|\le 2^{\frac{1}{n-1}}$ za svaki prirodan broj $k$.

Dokaz: Za vežbu.

Iz teorema 6 i 7 zaključujemo da tačka $c\in ℂ$ pripada Mandelbrotovom skupu ako i samo ako je orbita $\{f_c^n(0)\}$ ograničena kružnicom poluprečnika $2$. Ova činjenica će biti od izuzetne koristi prilikom crtanja Mandelbrotovog skupa.

Anatomija Mandelbrotovog skupa

Mandelbrotov skup je definisan kao skup svih kompleksnih vrednosti $c$ za koje je Žulijev skup funkcije $f_c$ povezan. Iako na prvi pogled deluje da je Mandelbrotov skup vezan samo za specifičnu osobinu Žulijevog skupa, ispostavlja se da Mandelbrotov skup sadrži u sebi mnogo više informacija o Žulijevom skupu. U narednim redovima će biti izneto bez dokaza nekoliko zanimljivih činjenica o vezama Žulijevog i Mandelbrotovog skupa.

Posmatranjem slike Mandelbrotovog skupa, može se uočiti da veliku površinu zauzima figura koja liči na ispunjenu „kardioidu“, za koju su zakačeni manji diskovi. Tačke $c$ u ispunjenoj „kardioidi“ odgovaraju funkcijama $f_c$ koji imaju privlačeću fiksnu tačku. Algebarski, ovo se može okarakterisati kao $f_c(z)=z$ i $|f{\prime }_c(z)|<1$. Na samoj „kardioidi“ očekivano bi bilo da važi $f_c(z)=z$ i $|f{\prime }_c(z)|=1$ tj. $|f{\prime }_c(z)|=e^{2\pi i\theta }$ za neko realno $0\le \theta \le 1$. Odavde dobijamo sistem $$\begin{array}{cc}\hfill z^2+c& =z\hfill \\ \hfill 2z& =e^{2\pi it}.\hfill \end{array}$$ Rešenje navedenog sistema po $c$ je $c(\theta )=e^{2i\theta }/2-e^{4i\theta }/4$, što nam govori da je „kardioida“ zaista kardioida.

Na sličan način možemo odrediti parametar $c$ za koji Žulijev skup ima periodičnu privlačeću tačku sa periodom dva. Naime, ovo odgovara uslovima $f_c^2(z)=z$ i $|(f_c^2)\prime (z)|<1$. Opet bi bilo očekivano da na granici traženog skupa važi jednakost $|(f_c^2)\prime (z)|=1$ umesto navedene nejednakosti, što nas dovodi do sistema $$\begin{array}{cc}\hfill (z^2+c{)}^2+c& =z\hfill \\ \hfill 4z(z^2+c)& =e^{2\pi it},\hfill \end{array}$$ čije rešenje je $c(\theta )=-1+\frac{1}{4}{e}^{2\pi i\theta }$, što predstavlja parametrizaciju kružnice koja dodiruje kardioidu u tački $c=-\frac{3}{4}$.

Nastavljanjem opisanog procesa, možemo dobiti¹⁰ parametrizaciju dva diska koji sadrže parametre $c$ takve da $f_c$ poseduje periodičnu privlačeću tačku sa periodom tri. I ova dva diska dodiruju kardioidu…

Kao što vidimo, skup svih parametara $c$ takvih da polinom $f_c$ poseduje periodičnu privlačeću tačku nekog perioda $p\in \mathbb{N}$ veoma je interesantan. Ovaj skup označavamo sa $H_{ℳ}$. Za razumevanje skupa $H_{ℳ}$ od ključne važnosti je teorema koju je 1905. godine dokazao Fatou, a koju navodimo bez dokaza:

Teorema 8. Svaka privlačeća periodična tačka nekog polinoma privlači barem jednu kritičnu tačku.

Iz teoreme 8 direktno sledi da polinom $f_c$ može imati najviše jednu privlačeću tačku, kao i da je $H_{ℳ}\subset ℳ$. Takođe, može se dokazati da je skup $H_{ℳ}$ otvoren. Prema tome, nameće se odmah pitanje: da li je $H_{ℳ}=intℳ$? Ovo pitanje i dalje nema odgovora.

Povezane komponente skupa $H_{ℳ}$ nazivamo hiperboličke komponente ili mu atomi. Svaka hiperbolička komponenta sačinjena je od parametra $c$ za koji odgovarajući Žulijev skup ima privlačeću periodičnu tačku sa periodom $p$. Zbog toga govorimo o periodu hiperboličke komponente.

U okolini hiperboličke komponente perioda $p$, a van nje, nalaze se parametri koji određuju Žulijev skup sa periodičnom odbijajućom tačkom perioda $p$. Na samoj granici hiperboličke komponente nalaze se parametri koji određuju Žulijev skup sa periodičnom neutralnom tačkom perioda $p$. Što se više približavamo središtu hiperboličke komponente, to će multiplikator odgovarajuće periodične tačke biti manji.

U samom središtu hiperboličke komponente, nalazi se tačka koju nazivamo centar hiperboličke komponente ili nukleus mu atoma, i koja odgovara vrednosti $c$ za koji odgovarajući Žulijev skup ima superprivlačeću periodičnu tačku, odnosno periodičnu tačku čiji multiplikator je $0$. Kako je izvod polinoma $f_c(z)$ po $z$ jednak $2z$, tačka $z$ može biti superprivlačeća ako i samo ako je $0$. Odavde sledi da je tačka $c$ nukleus neke hiperboličke komponente sa periodom $k$ ako i samo ako je $f_c^k(0)=0$. Odavde se dobija niz polinoma: $$\begin{array}{cc}\hfill f_c^1(0)& =c\hfill \\ \hfill f_c^2(0)& =c+c^2\hfill \\ \hfill f_c^3(0)& =c+c^2+2c^3+c^4\hfill \\ \hfill f_c^4(0)& =c+c^2+2c^3+5c^4+6c^5+6c^6+4c^7+c^8\hfill \\ \hfill ⋮\end{array}$$ čija rešenja odgovaraju centrima hiperboličkih komponenti.

Neka je $H_p$ hiperbolička komponenta sa periodom $p$ koja dodiruje kardioidu u tački $c_p$. Zamislimo da se tačka $c$ nalazi u kardioidi, u bliznini komponente $H_p$ i da se kreće prema tački $c_p$. Tada se uočavaju sledeći fenomeni:

1. Dok je $c$ u unutrašnjosti kardioide, u skupu $𝒥$ se nalazi jedna atraktivna fiksna tačka $w$. Tačke u okolini tačke $w$ „spiralno“ teže ka tački $w$ pri iteracijama funkcije $f$. Što se više tačka $c$ približava tački $c_p$, to se Žulijev skup više „cepa“ na $p$ komponenti.
2. Kada $c$ stigne u tačku $c_p$, tada se $c$ nalazi na granici kardioide i komponente $H_p$. Kako je $w$ neutralna, to je $f_c\prime (w)=e^{i\theta }$ što znači da $f_c$ deluje na okolinu tačke $w$ tako što je rotira za ugao $\theta$. Sada se Žulijev skup sastoji od $p$ komponenti koje se dodiruju u tački $w$.
3. Kada $c$ prođe tačku $c_p$, i uđe u hiperboličku komponentu $H_p$ tačka $w$ postaje odbijajuća, i pojavljuje se $p$ privlačećih tačaka $w_0,\dots w_{p-1}$ u okolini tačke $w$, pri čemu su tačke $w_0,\dots w_{p-1}$ numerisane na osnovu položaja u odnosu na $w$, u smeru suprotnom od kazaljke na satu. Skup $\{w_0,\dots w_{p-1}\}$ je orbita tačke $w_0$, i važi $f_c:w_i\mapsto w_{i+q}$ za neko prirodno $q$, gde se indeksi uzimaju po modulu $p$.

Svaku hiperboličku komponentu koja „dodiruje“ kardioidu možemo označiti razlomkom $q/p$, gde je $p$ period hiperboličke komponente, a $q$ „ugao rotacije“ hiperboličke komponente opisan u tački 3 sa prethodne liste.

Na „vrhu“ svake $q/p$ hiperboličke komponente nalazi se antena koja se račva na tačno $p$ grana. Ako granu koja je povezana sa hiperboličkom komponentom obeležimo sa $A_0$, a ostale grane sa oznakama $A_1,\dots A_{p-1}$, krećući se pritom u smeru suprotnom od kazaljke na satu, tada će grana $A_q$ uvek biti najkraća.

Reparametrizacija Mandelbrotovog skupa

U prethodnom delu ovog teksta pokazano je da mnoge osobine Žulijevog skupa ${𝒥}_{f_c}$ zavise od položaja tačke $c$ u odnosu na Mandelbrotov skup. Iz teoreme 5, sledi da je svaki Žulijev skup kvadratnog polinoma sličan Žulijevom skupu polinoma $f_c\left(c\right)$ za neki kompleksan broj $c$. Međutim, kvadratni polinomi nisu morali biti parametrizovani baš familijom polinoma oblika $z^2+c$. Svaka druga familiju polinoma koja zavisi od jednog parametra i za koju važi da je svaki kvadratni polinom afino konjugovan barem jednom polinomu iz te familije, bila bi jednako dobra. I u tom slučaju bi Mandelbrotov skup bio definisan kao skup svih parametara za koje je odgovarajući Žulijev skup povezan, ali bi tada Mandelbrotov skup sasvim drugačije izgledao. U nastavku teksta navedeno je nekoliko alternativnih parametrizacija kvadratnih polinoma, i pokazano je kako u tim parametrizacijama izgleda Mandelbrotov skup.

Alfa parametrizacija je data sa $g_{\alpha }(z)=z^2+{\alpha }^{-1}$. Veza između „standardne“ parametrizacije i alfa parametrizacije je očigledna: tačka $w$ pripada Mandelbrotovom skupu u „standardnoj“ parametrizaciji ako i samo ako tačka $w^{-1}$ pripada Mandelbrotovom skupu u alfa parametrizaciji. Geometrijski gledano, navedena veza između parametara predstavlja kompoziciju inverzije u odnosu na jediničnu kružnicu centriranu u nuli, i konjugacije (osne simetrije u odnosu na realnu pravu). Zbog ovakve veze, kardioioda sa granice Mandelbrotovog skupa u „standardnoj“ parametrizcaiji odgovara krivi oblika suze u alfa parametrizaciji.

Ako se pre inverzije izvrši translacija za $1/4$, tada se kardioida slika u parabolu. Ovakvo preslikavanje odgovara beta parametrizaciji datoj sa $$g_{\beta }(z)=z^2+\frac{1}{\beta +1/4}.$$

Još jedna uobičajena parametrizacija je lambda parametrizacija data sa $h_{\lambda }(z)=\lambda z(1-z)$. Lako se dobija veza parametra $c$ iz „standardne“ parametrizacije Mandelbortovog skupa i parametra $\lambda$ data sa $$c=\frac{\lambda }{2}-\frac{{\lambda }^2}{4},$$ pa je za ovakvu parametrizaciju Mandelbrotov skup ustvari skup svih kompleksnih parametara $\lambda$ za koje orbita ${𝒪}_{h_{\lambda }}\left(1/2\right)$ ostaje ograničena.

Kako je parametrizacija kardioide na granici Mandelbrotovog skupa data sa $e^{i\theta }/2-e^{2i\theta }/4$, a parametrizacija jedinične kružnice data sa $e^{i\theta }$, sledi da glavnoj kardioidi Mandelbrotovog skupa u „standardnoj“ parametrizaciji odgovaraju dve¹¹ kružnice u lambda parametrizaciji. Navedene kružnice imaju poluprečnik $1$ i centrirane su u tačkama $\lambda =0$, odnosno $\lambda =2$. Tačka $\lambda =1$ u kojoj se kružnice dodiruju odgovara „špicu“ kardioide.

Inverzijeom kompleksne ravni oko jedinične kružnice sa centrom u nuli, jedna od navedenih kružnica ostaje invarijantna, dok se druga slika u njenu unutrašnjost. Na ovaj način se dobija prva od naredne dve figure. Ako se pre inverzije izvrši translacija ulevo za $1$, tada se navedene dve kružnice preslikavaju u dve paralelne prave. Na ovaj način se dobija druga od naredne dve figure.

Zapravo, lambda parametrizacija $h_{\lambda }(z)=\lambda z(1-z)$ je prva parametrizacija koju je Mandelbrot koristio kada je otkrio skup nazvan po njegovom imenu. Mandelbrot je kasnije o svom otkriću, između ostalog, napisao sledeće:

A first test used the quadratic map in the alternative form $z\mapsto \lambda z(1-z)$. After few iteration steps on a rough grid, we saw that the set $ℳ$ includes the very crude outline of the two discs $\left|\lambda \right|<1$ and $|\lambda -2|<1$. Two lines of algebra confirmed that these discs were to be expected here, and that the method was working. We also saw, on the real line to the right and left of the above discs, the crude outlines of round blobs which I call "atoms" today…

Nije slučajno što je Mandelbrot prvo posmatrao baš lambda parametrizaciju. Čitaoci koji su upoznati sa diferencijalnim jednačinama, vide da je lambda parametrizacija dobro poznata logistička jednačina¹².

Multibrot skup

Mandelbrotov skup u sebi krije mnoge zanimljive tajne. I sam oblik Mandelbrotovog skupa je dovoljno zanimljiv i vizuelno privlačan, da bi nas naveo da krenemo da eksperimentišemo sa definicijom Mandelbrotovog skupa u nadi da ćemo pronaći nekakve slične objekte.

Po teoremi 6, Mandelbrotov skup se može definisati kao skup kompleksnih brojeva $c$ za koje niz $f_c(0),f_c^2(0),\dots ,f_c^k(0)$ ostaje ograničen, gde je $f_c$ polinom $z^2+c$. Pošto smo dovoljno radoznali i želimo da eksperimetišemo, mi možemo promeniti gore navedenu definiciju Mandelbrotovog skupa tako što ćemo posmatrati iteracije polinoma $f_{c,n}(z)=z^n+c$. Time stižemo do definicije multibrot¹³ skupa. Preciznije, multibrot skup reda $n$, u oznaci ${ℳ}_n$, definišemo kao $${\mathcal{M}}_n=\{c\in \mathbb{C}\hspace{0.17em}|\hspace{0.17em}{f}_{c,n}^k(0)\to ̸\mathrm{\infty },\hspace{0.25em} (k\to \mathrm{\infty })\},$$ gde je $f_{c,n}$ polinom $z^n+c$.

Iscrtavanjem multibrot skupova, vidi se da oni dosta liče na Mandelbrotov skup: u centru skupa dominira velika površina - glavna hiperbolička komponenta (koja odgovara ispunjenoj kardioidi Mandelbrotovog skupa), za koju su zakačene manje hiperboličke komponente.

Glavnu hiperboličku komponentu čine svi parametari $c$ za koje polinom $f_{c,n}$ ima privlačeću tačku perioda 1, odnosno privlačeću fiksnu tačku. Ponovo, na granici hiperboličke komponente, očekivano je da se nalaze parametri koji određuju polinome sa neutralnom fiksnom tačkom. Odavde se dobijaju dva uslova $$\begin{array}{cc}\hfill f_{c,n}(z)& =z\hfill \\ \hfill |f{\prime }_{c,n}(z)|& =1.\hfill \end{array}$$

Koristeći drugi uslov dobijamo da je $n{z}^{n-1}=e^{i\theta }$ za neko realno $\theta$, iz čega sledi da je $z=\sqrt[n-1]{k^{-1}{e}^{i\theta }}$. Zamenjući poslednju jednakost u prvi uslov, odnosno u jednačinu $z^n+c=z$, dobijamo da je $$c\left(\theta \right)={\left(\frac{e^{i\theta }}{n}\right)}^{\frac{1}{n-1}}-{\left(\frac{e^{i\theta }}{n}\right)}^{\frac{n}{n-1}}.$$

Pritom, da bi kriva bila zatvorena, njen izvod mora da namota barem jedan krug. Pri gornjoj parametrizaciji to će se desiti ako parametar $\theta$ prođe intervalom $[0,2n\pi ]$. Linearnom reparametrizacijom, dobijamo malo lepšu parametrizaciju krive $c$: $$c\left(\theta \right)=\frac{e^{i\theta }}{n^{\frac{1}{n-1}}}-\frac{e^{in\theta }}{n^{\frac{n}{n-1}}}\theta \in [0,2\pi ].$$

Parametrizacija granice glavne hiperboličke komponente može se dalje iskoristiti za pronalaženje najvećeg kruga sa centrom u $0$ koji se nalazi unutar hiperboličke komponente, odnosno za pronalaženje upisanog kruga multibrot skupa. Za to je dovoljno samo primetiti da izraz $${\left|c\left(\theta \right)\right|}^2=\frac{1}{n^{\frac{2}{n-1}}}-\frac{1}{n^{\frac{n}{(n-1{)}^2}}}(e^{(1-k)i\pi }+e^{(k-1)i\pi })+\frac{1}{n^{\frac{2n}{n-1}}}$$ ima minimum $1/n^{\frac{2}{n-1}}-2/n^{\frac{n}{(n-1{)}^2}}+1/n^{\frac{2n}{n-1}}={(n^{-\frac{1}{n-1}}-n^{-\frac{n}{n-1}})}^2$. Upravo je ovaj minimum kvadrat poluprečnika traženog kruga.

Na osnovu teoreme 7 sledi da je multibrot skup ${ℳ}_n$ ograničen kružnicom poluprečnika $2^{\frac{1}{n-1}}$. Ovakav krug se naziva opisani krug multibrot skupa.

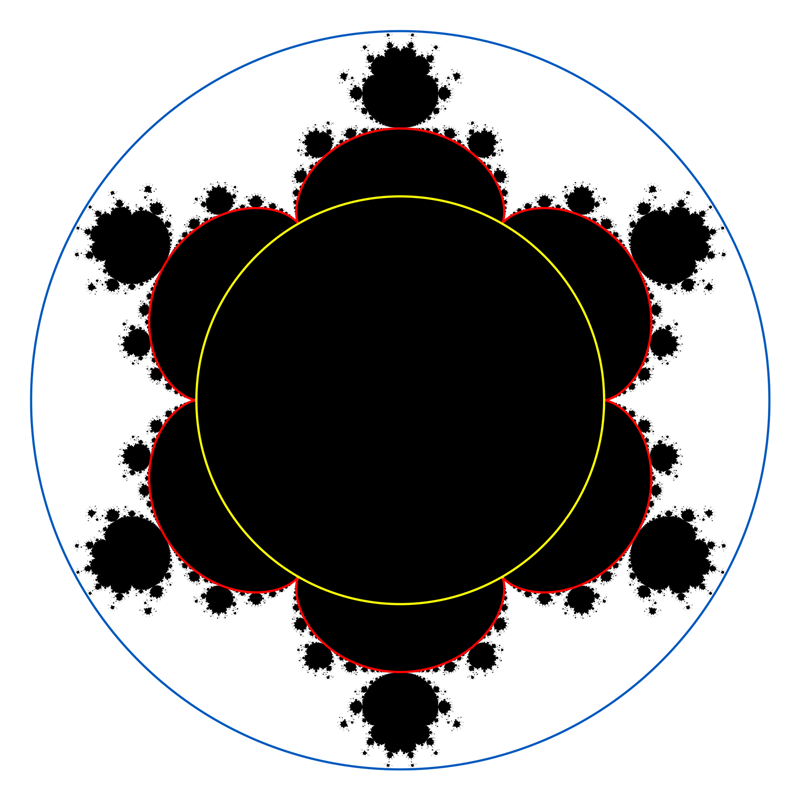
Puštanjem limesa kad $n\to \infty$ u izraz za parametrizaciju granice glavne hiperboličke komponente i izraz za poluprečnik kružnice koja ograničava multibrotov skup, dobija se da multibrotov skup „teži“ krugu poluprečnika $1$.

Odavde se lako može izvesti i jedna gruba procena površine multibrotovog skupa, ako multibrotov skup uopšte ima površinu. Koristeći uobičajan postupak sa Stoksovom teoremom primenjenom na formu $xdy-ydx$, dobijamo da je površina glavne hiperboličke komponente $H_1$ data sa $$\begin{array}{cc}\hfill A\left(H_1\right)& =\underset{H}{\int }dxdy=\frac{1}{2}\underset{\partial H}{\int }xdy-ydx\hfill \\ \hfill & =\frac{1}{2}\underset{0}{\overset{2\pi }{\int }}2(n+1)k^{-\frac{n+1}{n-1}}{sin}^2\left(\frac{\theta (n-1)}{2}\right)d\theta \hfill \\ \hfill & =\pi (n+1)n^{-\frac{n+1}{n-1}}\hfill \end{array}$$

Sa druge strane, multibrot ${ℳ}_n$ skup je ograničen kružnicom polprečnika $2^{\frac{1}{n-1}}$ pa je njegova površina manja od $\pi 2^{\frac{2}{n-1}}$. Iz svega ovoga sledi gruba procena: $$\pi (n+1)k^{-\frac{n+1}{n-1}}\le A\left(M_n\right)\le \pi 2^{\frac{2}{n-1}}.$$ Tačnost navedene procene se uvećava sa rastom broja $n$.

Posmatranjem slike skupa ${ℳ}_n$, deluje kao da je taj skup uvek simetričan u odnosu na realnu osu. Ovo se veoma lako dokazuje korišćenjem indukcije: Ako za $k$-tu iteraciju polinoma $f$ važi $f_{\overline{c},n}^k\left(0\right)=\overline{f_{c,n}^k\left(0\right)}$, tada je $$f_{\overline{c}}^{k+1}\left(0\right)={\left(f_{\overline{c}}^k\left(0\right)\right)}^n+\overline{c}=\overline{{\left(f_c^k\left(0\right)\right)}^n+c}=\overline{f_c^{k+1}\left(0\right)}.$$ Kako se baza indukcije trivijalno proverava, zaključujemo da za svako prirodno $k$ važi $f_{\overline{c},n}^k\left(0\right)=\overline{f_{c,n}^k\left(0\right)}$. Kompleksan broj teži beskonačnosti ako i samo ako njegov konjugat takođe teži beskonačnosti, pa po definiciji multibrot skupa zaključujemo da je taj skup simetričan u odnosu na realnu osu.

Analogno se dokazuje da skup ${ℳ}_n$ poseduje rotacionu simetriju reda $n-1$.

Čitaoci bi trebalo da imaju na umu da su multibrot skupovi ${ℳ}_n$ za $n\ge 3$ u vezi sa Žulijevim skupovima odgovarajućeg stepena, kao što postoji veza Mandelbrotovog skupa $ℳ={ℳ}_2$ i polinoma drugog stepena. Jedina razlika je u tome što, za razliku od polinoma oblika $z^2+c$, nisu svi polinomi stepena $n\ge 3$ afino konjigovani nekom polinomu oblika $z^n+c$.

Potencijal Žulijevog i Mandelbrotovog skupa

Jedan od osnovnih rezultata kompleksne analize je Rimanova teorema o uniformizaciji koja glasi: Svaka prosto povezana Rimanova mnogostrukost je konformno ekvivalentna jednoj od sledeće tri mnogostrukosti

• otvorenom jediničnom disku,
• kompleksnoj ravni,
• Rimanovoj sferi.

Iz ove teoreme sledi da za prosto povezan kompaktan skup $K$ postoji jedinstven pozitivan broj $r$ i jedinstveno preslikavanje $\varphi :ℂ\backslash K\mapsto ℂ\backslash {𝔻}_r$, takvo da je $\Phi$ izometrija sa osobinom da $\varphi \left(z\right)/z\to 1$ kad $z\to \infty$. Ovakvo $r$ nazivamo kapacitet skupa $K$. Navedeni objekti su veoma korisni za proučavanje Žulijevih skupova, što pokazuje sledeća teorema:

Teorema 9. Neka je $f:ℂ\to ℂ$ moničan polinom stepena $d\ge 2$, takav da je Žulijev skup ${𝒦}_f$ povezan. Tada skup ${𝒦}_f$ ima kapacitet 1 i konformna reparametrizacija ${\varphi }_f:ℂ\backslash K_f\mapsto ℂ\backslash 𝔻$ konjuguje funkciju $f$ sa funkcijom $z\mapsto z^d$.

Sama funkcija ${\varphi }_f$ iz prethodne teoreme se naziva Betherovim¹⁴ preslikavanjem. Linije $\left|{\varphi }_f\right|=const$. nazivamo ekvipotencijalne linije, dok linije $arg\left(\varphi \left(z\right)\right)=const$. nazivamo spoljašnji zraci.

Neka je $f\left(z\right)=z^n+\dots +a_{1}z+a_0$ moničan polinom takav da je $K_f$ povezan skup. Neka je za $z\in ℂ\backslash K_f$ definisan niz $z_k=f^k\left(z\right)$. Iz jednakosti ${\varphi }_f\left(z_{k+1}\right)={\left({\varphi }_f\left(z_k\right)\right)}^n$ sledi da je preslikavanje ${\varphi }_f$ dato beskonačnim proizvodom $${\varphi }_f\left(z\right)=z\prod _{k=0}^{\infty }{(1+\frac{a_{d-1}}{z}+\cdots +\frac{a_0}{z^n})}^{1/d^{k+1}}.$$ Pritom se u prethodnom izrazu uzima grana funkcije ${(1+w)}^{1/d^{k+1}}$ koja $0$ šalje u $1$. Navedeni proizvod brzo konvergira što se može iskoristiti za crtanje Žulijevog skupa.

Funkcija $G_f\left(z\right)=log\left|{\varphi }_f\left(z\right)\right|$ zadovoljava naredne osobine koje se lako proveravaju

1. Skup vrednosti funkcije $G_f$ je ${ℝ}^{+}$,
2. $G_f$ je harmonijska funkcija,
3. $G_f\left(z\right)=log\left|z\right|+𝒪\left(1\right)$ kad $z\to \infty$,
4. $G_f\left(z\right)\to 0$ kada $d(z,K_f)\to 0$,
5. $G_f\left(f\left(z\right)\right)=n\cdot G_f\left(z\right)$, gde je $n=degf$,

zbog čega se funkcija $G_f$ naziva potencijal¹⁵ Žulijevog skupa ${𝒦}_f$ ili Grinova funkcija¹⁶ skupa ${𝒦}_f$.

Štaviše, funkcija $G_f$ je u potpunosti određena osobinama (1), (3) i (5). Naime, iz ovih osobina direktno sledi da je $$G_f\left(z\right)=\underset{k\to \infty }{lim}\frac{1}{n^k}log|f^k(z)|.$$

Preslikavanje $\varphi$ iz teoreme se može iskoristiti za konstruisanje analognog preslikavanja za Mandelbrotov skup. Tačnije, važi sledeća teorema koju navodimo bez dokaza:

Teorema 10. Neka je $\Phi :ℂ\backslash ℳ\to ℂ$ definisano sa $\Phi \left(c\right)={\varphi }_{f_c}\left(c\right)$, gde je $f_c\left(z\right)=z^2+c$. Tada je $\Phi$ izomorfizam između $ℂ\backslash ℳ$ i $ℂ\backslash 𝔻$.

Iz ove teoreme možemo zaključiti da je Mandelbrotov skup $ℳ$ povezan skup. I dalje se ne zna da li je Mandelbrotov skup lokalno povezan¹⁷ skup?

Crtanje Žulijevog i Mandelbrotovog skupa

Kako su skupovi koji su do sada opisani sačinjeni od beskonačno tačaka, a čovek i računari mogu izvršiti samo konačno mnogo operacija, potrebno je izabrati konačno mnogo tačaka kompleksne ravni da bi se ti skupovi nacrtali. Osnovna ideja svih algoritama za crtanje Žulijevog i Mandelbrotovog skupa je ta da se odabirom što većeg broja tačaka greška prilikom crtanja navedenih skupova smanjuje.

Za crtanje Žulijevog i Mandelbrotovog skupa, na slici dimenzija $w\cdot h$, potrebno je prvo izabrati pravougaouu oblast u kompleksnoj ravni čije se stranice odnose u razmeri $w:h$, gde su $w$ i $h$ prirodni brojevi. Zatim je potrebno tu oblast izdeliti na $w\cdot h$ manjih podudarnih kvadrata (piksela), i iz svakog kvadrata je potrebno izabrati po jednu tačku (na primer gornje levo teme kvadrata, ili sam centar kvadrata). Za fiksirane dimenzije velikog pravougaonika, uvećavanjem rezolucije slike, površina kvadrata će se smanjivati, a samim tim će se i „vernost“ slike uvećavati.

U nastavku ćemo piksele na slici obeležavati sa velikim štampanim slovima, dok ćemo odgovarajuće tačke u kompleksnoj ravni, obeležavati malim pisanim slovima (na primer, pikselu P odgovara tačka $p$, itd…).

Escape time metod

Najjednostavniji algoritam za crtanje Žulijevog skupa je poznat kao escape time algoritam. Ovaj algoritam se zasniva na teoremi 3, koja kaže da tačka $z$ pripada Žulijevom skupu ${𝒥}_f$ ako i samo ako njena orbita ostaje ograničena prilikom iteracija funkcije $f$. Po ovoj teoremi, za svaku polinomsku funkciju $f$ može se izračunati broj $R$ takav da $z\to \infty$ ako i samo ako postoji prirodno $k$ takvo da je $|f^k(z)|>R$. Ovakvo (i svako veće) $R$ nazivamo poluprečnik izlaska, a kružnicu centriranu u $0$ sa poluprečnikom $R$ nazivamo kružnica izlaska.

Ideja escape time algoritma je sledeća: Neka je $N$ fiksiran prirodan broj (na primer neka je $N=200$), koji označava maksimalan broj iteracija. Neka je Z proizvoljan piksel na slici, a $z$ kompleksan broj određen pikselom Z. Ako je $z>R$ onda sledi da tačka $z$ ne pripada ispunjenom Žulijevom skupu. Ako je $z\le R$, tada proveravamo da li je $f(z)>R$. Ako važi $f(z)>R$ tada ponovo sledi da $z$ ne pripada ispunjenom Žulijevom skupu. U suprotnom, proveravamo da li je $f^2(z)>R$… Ovaj proces ponavljamo sve dok ne stignemo do $N$-te iteracije tj. dok ne dostignemo maksimalan broj iteracija. Ako $f^N(z)<R$ tada smatramo da tačka $z$ pripada Žulijevom skupu, i piksel Z bojimo određenom, unapred zadatom, bojom (na primer crnom). Piksele koji određuju tačke van ispunjenog Žulijevog skupa bojimo nekom drugom bojom (na primer belom). Opisani postupak ponavljamo za svaki piksel na slici.

Za svaki piksel Z u slici, izvrši {
    z = kompleksni broj određen pikselom Z;
    k = 0;
    	
    Za (k=0; k < N; k++) {
        z = f(z);
        Ako je moduo broja z veći od R izađi iz petlje;
    }

    Ako je k = N oboji piksel Z u crno, u suprotnom oboji ga u belo;
}

Odmah se uviđa problem sa ovakvim algoritmom: Ako je $f^k(z)<R$ za $1\le k\le N$, tada ne znači da će $f^k(z)<R$, za svako $k\in \mathbb{N}$. Zbog ovoga, escape time algoritam obeležava neke piksele na slici kao da pripadaju ispunjenom Žulijevom skupu, iako oni zapravo ne pripadaju tom skupu. Povećavanjem maksimalnog broja iteracija, ova greška se smanjuje, ali se vreme izvršavanja algoritma uvećava.

Kako Žulijev skup sadrži neograničeno fine detalje, uvećavanje maksimalnog broja iteracija dovodi i do pojave šuma¹⁸, na samom Žulijevom skupu. Šum se može izbeći ako se slika iscrta u nekoliko puta većoj rezoluciji od željene, a zatim se umanji na željenu rezoluciju uz pomoć nekog naprednijeg algoritma za umanjenje slika.

U praksi je potrebno eksperimentalno doći do maksimalnog broja iteracija koji daje zadovoljavajuće rezultate.

Teoreme 6 i 7 daju osnovu escape time algoritma za Mandelbrotov skup. Ideja se sastoji u tome da se za svaki piksel C posmatra niz $f_c(0),f_c^2(0),f_c^3(0),\dots ,f_c^M(0)$, gde je $c$ kompleksan broj određen pikselom C, a $N$ maksimalan broj iteracija. Ako je navedeni niz ostao ograničen kružnicom poluprečnika $2$, tada smatramo da tačka $c$ pripada Mandelbrotovom skupu. U suprotnom smo sigurni da ona ne pripada Mandelbrotovom skupu.

Za svaki piksel C u slici, izvrši {
    c = kompleksni broj određen pikselom C;
    z = 0
    k = 0;
    	
    Za (k=0; k < N; k++) {
        z = f(z, c);
        Ako je moduo broja z veći od 2 izađi iz petlje;
    }

    Ako je k = N oboji piksel C u crno, u suprotnom oboji ga u belo;
}

I za ovaj algoritam važe isti komentari o maksimalnom broju iteracija kao i za prethodni algoritam.

Opisani algoritam za crtanje Mandelbrotovog skupa se direktno može preneti i na slučaj multibrot skupa. Dovoljno je samo umesto funkcije $f(z,c)=z^2+c$, koristiti funkciju $f(z,c)=z^n+c$.

Jasno je da su navedeni escape time algoritmi za iscrtavanje ispunjenog Žulijevog skupa odnosno Mandelbrotovog skupa skoro pa isti. Zbog toga ćemo se u nastavku ove sekcije posvetiti proučavanju algoritma za iscrtavanje Žulijevog skupa. Sve što se do kraja ove sekcije bude reklo o escape time algoritmu za iscrtavanje ispunjenog Žulijevog skupa može se direktno preneti na slučaj escape time algoritma za iscrtavanje Mandelbrotovog skupa…

U svim navedenim escape time algoritmima najviše vremena se utroši na tačke koje pripadaju ispunjenom Žulijevom odnosno Mandelbrotovom skupu (jer ove tačke prolaze kroz maksimalan broj iteracija). Postoje dva jednostavna načina da se navedeni algoritmi optimizuju.

• Prvi način je da se proveri periodičnost orbite tačke $z$. To se može uraditi tako što se prilikom svake iteracije vrednost $f^k(z)$ upoređuje sa vrednostima $f^{k-1}(z),f^{k-2}(z),\dots ,f^{k-l}(z)$. Na ovaj način će se detektovati predperiodične tačke sa periodom ne većim od $l+1$. Jasno je da se ovakvim pristupom troši dodatna memorija i dodatne instrukcije poređenja.
• Drugi način optimizacije escape time algoritma je karakterističan za Mandelbrotov skup. Znamo da glavna kardioida čini većinu površine Mandelbrotovog skupa, a znamo i parametrizaciju glavne kardioide. Prema tome, pre iteracije polinoma $f_c$, možemo veoma „jeftino“ proveriti da li tačka $c$ pripada glavnoj kardioidi. Ako je to slučaj, tada znamo da tačka $c$ pripada i Mandelbrotovom skupu. Primetimo da ova optimizacija ima smisla samo ako veliki deo naše slike pripada kardioidi.

Slike koje se dobijaju uz pomoć navedenog algoritma su jednobitne predstave ispunjenog Žulijevog skupa. Ovakve slike su odlične za primenu algoritma za detekciju ivica u naknadnoj obradi, čime se dobijaju slike Žulijevog skupa.

Najednostavnija modifikacija escape time algoritma, sastoji se u tome da tačke (tj. odgovarajuće piksele) Fatuovog domena bojimo na osnovu toga koliko im je iteracija bilo potrebno da izađu van kružnice izlaska. Jedina razlika novog algoritma u odnosu na prethodni je u poslednjoj liniji:

Ako je k = N oboji piksel Z u crno, u suprotnom oboji ga u L(k);

Za implementaciju ovakvog bojenja potrebno je definisati funkciju $L$ koja u zavisnosti od prirodnog broja $i$ vraća boju. Najjednostavniji izbor ovakve funkcije je linearna interpolacija dve boje: $$L(i)=\frac{i}{N}{B}_1+(1-\frac{i}{N})B_2$$

U gornjem izrazu $N$ je maksimalan broj iteracija, a $B_1$ i $B_2$ su unapred definisane boje¹⁹.

Drugi najjednostavniji izbor funkcije $L$ je L(k)=paleta_boja[k%B], gde je paleta_boja niz od B boja.

Rezultat ovakvog algoritma je slika poput naredne.

Kod ovakvog bojenja uočljive su jednobojne trake oko ispunjenog Žulijevog i Mandelbrotovog skupa. Ove trake se javljaju zbog toga što se za bojenje piksela koristi jedna celobrojna vrednost. Svim tačkama koje pripadaju jednoj traci bio je potreban isti broj iteracija da bi izašle van kružnice izlaska²⁰.

Iako su slike dobijene na ovaj način veoma zanimljive, bilo bi poželjno neprekidno obojiti Fatuov domen. Za ovakvo bojenje biće potreban broj iteracija i kroz koji je tačka prošla, kao i jedan realan broj $\lambda \in [0,1]$ koji će u nastavku biti određen.

Za određivanje vrednosti $\lambda$ može se iskoristiti moduo poslednje iteracije kao dodatnu informaciju. Primetimo da što veći moduo ima tačka $z$ to će se vrednost $f(z)=a_n{z}^n+a_{n-1}{z}^{n-1}+\dots +a_0$ sve više ponašati kao $a_n{z}^n$, jer $z^n$ raste brže od ostalih sabiraka u navedenom izrazu. Zbog toga se može smatrati da važi $f^k(z)\approx a_n^k{z}^{kn}$ za tačke $z$ sa dovoljno velikim moduom.

Fiksirajmo sada neko realno $T$ dovoljno veliko da procena iz prethodnog pasusa važi. Možemo pretpostaviti da je ovo $T$ veće od poluprečnika izlaska koje nam garantuje teorema 3. Sve tačke koje izađu van kružnice izlaska u nekoj iteraciji izaći će i van diska sa poluprečnikom $T$ u nekoj od narednih iteracija. Ako tačka $z$ ne pripada ispunjenom Žulijevom skupu tada postoji najveći prirodan broj $i$ takav da važi $|f^{i-1}(z)|<T$. Kako je $T$ veliko, po prethodnom pasusu zaključujemo da važi²¹ procena $T\le |f^i(z)|<T^n$. Sada, vrednost $\lambda$ možemo odrediti formulom $$\lambda =\frac{T^n-|f^i(z)|}{T^n-T}$$

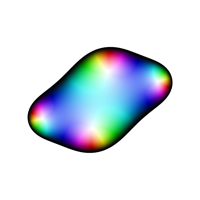
Funkcija $\mu =i+1-\lambda$ se može iskoristiti za definisanje funkcije bojenja $L$. Sa ovakvom funkcijom se dobijaju slike poput naredne.

Ipak navedena funkcija nije diferencijabilna u tačkama²² $z$ za koje važi $|f^i(z)|=T$. Da bi se glatko obojio Fatuov domen, dovoljno je koristiti parametar $\lambda$ definisan sa $$\lambda ={log}_{n}log\left|f^i\left(z\right)\right|,$$ gde je $n$ stepen polinoma $f$. Uz pomoć glatkog bojenja, dobija se slika poput naredne.

Izgled slike u mnogome zavisi i od izbora palete koja se koristi za bojenje. Jasno je da je broj mogućih paleta skoro pa beskonačan.

Potpuna ista funkcija glatkog bojenja se može iskoristiti za bojenje komplementa Mandelbrotovog skupa, što je prikazano na narednoj slici.

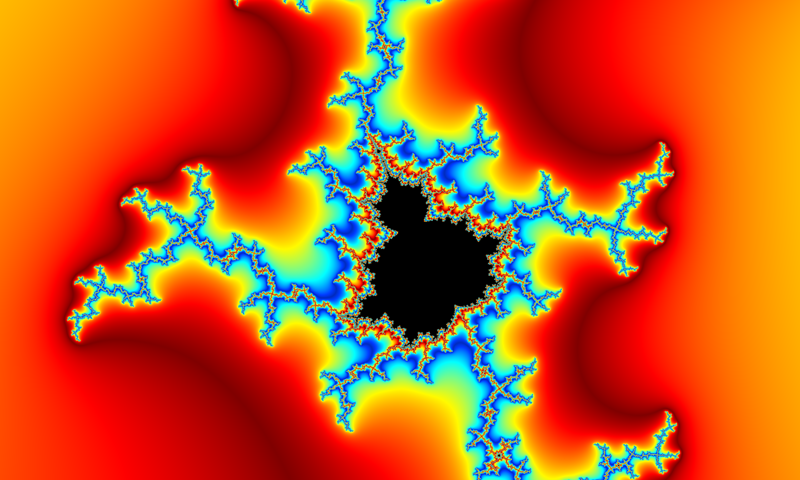
Suština navedena tri algoritma za bojenje Fatuovog skupa, je u tome da se tačka Fatuovog skupa oboji na osnovu udaljenosti njene $i$-te iteracije od $0$, gde je sa $i$, kao i do sada, označen najmanji broj iteracija potrebnih da bi tačka $z$ izašla van kružnice izlaska. Ipak, za bojenje Fatuovog domena se može iskoristi i neku drugi podatak o $i$-toj iteraciji. Na primer, to može biti i argument $i$-te iteracije. U praksi, dovoljno je izmeniti osnovni algoritam za crtanje Žulijevog skupa, tako što će se za funkciju bojenja uzeti neka funkcija koja zavisi samo od argumenta „poslednje“ iteracije.

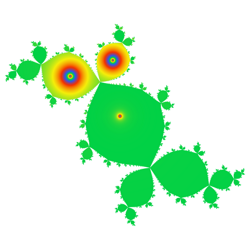
Kao što se vidi na prethodnoj figuri, pri ovakvom bojenju su prisutni „prelomi“ boja na mestu ekvipotencijalnih linija. Ovi prelomi su prisutni na slici jer nisu sve tačke prošle kroz isti broj iteracija. Tačkama koje su bliže Žulijevom skupu, bio je potreban veliki broj iteracija da bi izašle van kružnice izlaska. Zbog toga su prilikom tih iteracija takve tačke puno puta „namotane“ oko $0$, što je dovelo do toga da se bojenje ovih tačaka učestalo smenjuje. S druge strane, tačkama koje se nalaze dalje od Žulijevog skupa, potrebno je samo par iteracija da bi izašle van kružnice izlaska, zbog čega se bojenje tih tačaka smenjuje samo par puta.

Jednostavan način da se izbegne navedeni efekat, je da se iz algoritma obriše naredba koja prekida iteracije u slučaju da tačka izađe van kružnice izlaska. Na ovaj način će sve tačke sa slike proći kroz isti broj iteracija. Pseudokod sada izgleda ovako:

Za svaki piksel Z u slici, izvrši
{
    z = kompleksni broj određen pikselom Z;
    k = 0;
    	
    Za (k=0; k < N; k++) {
        z = f(z);
    }

    Ako je k = N oboji piksel Z u crno, u suprotnom oboji ga u L(Arg(z));
}

Štaviše, na opisani način možemo obojiti i ispunjen Žulijev skup. Dovoljno je samo poslednju liniju u prethodnom pseudokodu zameniti linijom

Oboji piksel Z u L(Arg(z));

Uz ovakav algoritam se slabije uočava oblik (ispunjenog) Žulijevog skupa, ali se odlično uočava kako se itracije polinoma dejstvuju na kompleksnu ravan.

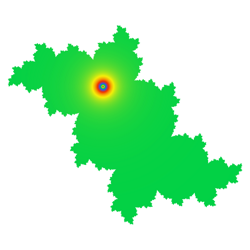
Kako je i sama funkcija $Arg:{ℂ}^{*}\to {𝕊}^1$ neprekidna, lako se može implementirati i neprekidno bojenje na osnovu argumenta poslednje iteracije, što je prikazano na sledećoj slici.

Koristeći i moduo i argument „poslednje“ iteracije, možemo izdeliti Fatuov skup na krivolinijske pravugaonike u kojima uvodimo lokalni koordinatni sistem. To činimo na sledeći način: neka je $z$proivoljna tačka Fatuovog skupa, i $i$ broj iteracija potreban da bi tačka $z$ izašla van kruga izlaska. Tada tački $z$ dodeljujemo koordinate $$({log}_d({log}_R|f^i\left(z\right)|),\frac{Arg\left(f^i\left(z\right)\right)}{2\pi }).$$

Ove koordinate se dalje mogu iskoristiti za „popločavanje“ Fatuovog domena nekom željenom slikom.

Sličan efekat „popločavanja“ Fatuovog domena se može izvesti i uz pomoć Betherove funkcije.

Metod određivanja udaljenosti

Pretpostavimo da postoji glatko preslikavanje $F:{ℝ}^n\to ℝ$ takvo da je skup $F^{-1}\left(0\right)$ jedna kriva. Često je korisno je pronaći udaljenost proizvoljne tačke prostora od ove krive. Ovaj zadatak je često i nemoguć zbog komplikovanih izraza koji se javljaju u računu, ali postoji jedna jednostavna aproksimacija rešenja. Neka je $y$ tačka takva da je $\nabla F\left(y\right)\ne 0$, i neka je $x$ tačka koja pripada krivoj $F^{-1}\left(0\right)$. Tada po Tejlorovoj formuli važi $$0=F\left(x\right)=F\left(y\right)+\nabla F\left(y\right)\cdot (x-y)+ℴ\left(\parallel x-y\parallel \right).$$ Ako su tačke $x$ i $y$ dovoljno blizu, tada možemo zanemariti sabirak $ℴ\left(\parallel x-y\parallel \right)$ pa jednostavnim računom dobijamo da je $$\parallel x-y\parallel =\frac{\left|F\left(y\right)\right|}{\parallel \nabla F\left(y\right)\parallel }.$$

Ako ovaj metod primenimo da Grinovu funkciju Žulijevog skupa ${𝒦}_f$ (uz ogovarajuću identifikaciju $ℂ$ sa ${ℝ}^2$), dobijamo formulu $$d_{{𝒦}_f}\left(z\right)=\underset{k\to \infty }{lim}\frac{\left|f^k\left(z\right)\right|log\left|f^k\left(z\right)\right|}{\left|\left(f^k\right)\prime \left(z\right)\right|}.$$

U praksi, funkciju $d_{{𝒦}_f}$ računamo kao $$d_{{𝒦}_f}\left(z\right)=\frac{\left|f^N\left(z\right)\right|log\left|f^N\left(z\right)\right|}{\left|\left(f^N\right)\prime \left(z\right)\right|},$$ gde je $N$ veliki prirodan broj. Pritom, izvod $\left(f^N\right)\prime$ lako možemo izračunati pravilom za izvod kompozicije funkcija. Tako dobijamo naredni algoritam:

Za svaki piksel Z u slici, izvrši {
    z = kompleksni broj određen pikselom Z;
    dz = 1; 
    k = 0;
    	
    Za (k=0; k < N; k++) {
        z = f(z);
        dz = dz * f'(z);
    }

    Ako je |z| veće od R {
    	d = |z| * log(|z|) / dz;
    	Oboji piksel Z u nijansu određenu brojem d;
    } u suprotnom {
        Oboji piksel Z u crno;
    }
}

Neznatnom modifikacijom navedenog algoritma dobija se algoritam koji crta Mandelbrotov skup metodom određivanja udaljenosti.

Na slikama iscrtanim sa ovom metodom bolje se uočavaju fini detalji Žulijevog i Mandelbrotovog skupa, nego što je to slučaj kod slika dobijenih sa escape time tehnikom.

Budabrot metod

Budabrot (eng. buddhabrot) je naziv tehnike crtanja orbita koje se javljaju u Mandelbrotovom skupu pri iteracijama polinoma. Tačnije, budabrot tehnikom se crtaju orbite tačaka koje se ne nalaze u Mandelbrotovom skupu. Uz pomoć ove tehnike se dobijaju slike poput naredne.

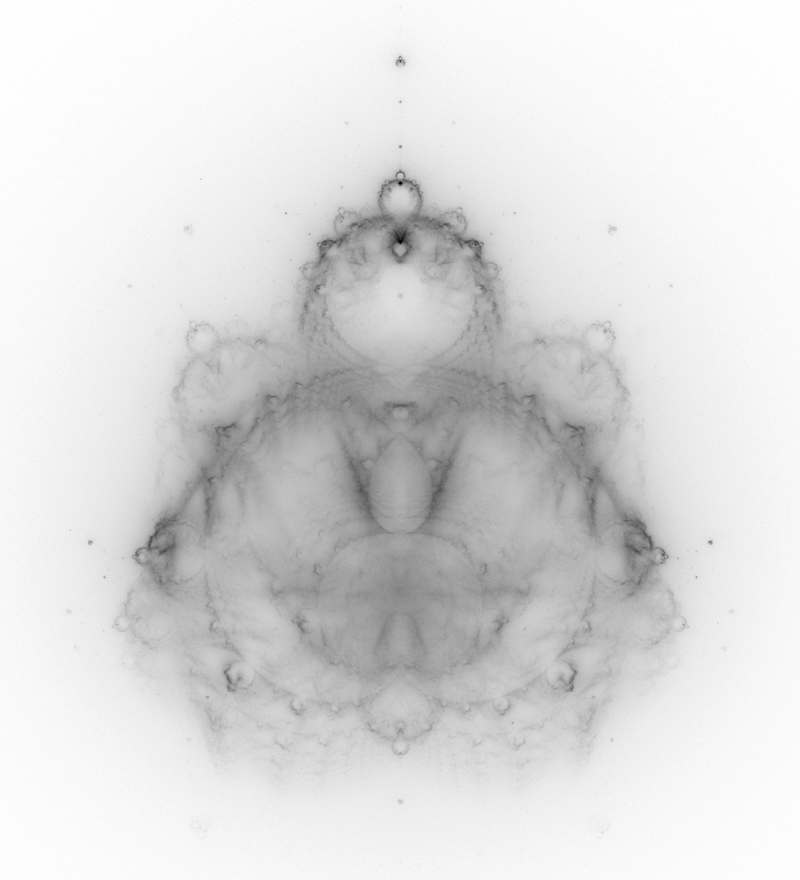
Budabrot tehniku je prvi put upotrebila Melinda Grin 1993. godine [5]. Crtež koji se dobija uz pomoć budabrot tehnike, podesća na Budu²³ koji sedi, po čemu je ova tehnika dobila ime.

Postupak za crtanje budabrot slike je sledeći: Prvo se kreira niz celobrojnih brojača odgovaraju pikselima na slici koja se crta. Zatim se nasumično odabira tačka $c$ iz kompleksne ravni, za koju se, uz pomoć escape time algoritma, proverava da li pripada Mandelbrotovom skupu. Ako $c$ pripada Mandelbrotovom skupu, tada se ponovo bira tačka $c$. Ako tačka $c$ ne pripada Mandelbrotovom skupu, tada se na osnovu njene orbite uvećavaju odgovarajući brojači, tako što se za svako pojavljivanje tačke $w$ iz orbite, uveća brojač odgovarajućeg piksela W. Kada se dovoljno nasumičnih tačaka odabere, opisani postupak se prekida, a zatim se kreira grayscale slika tako što se svaki piksel boji u nijansu sive koja se određuje na osnovu broja u njemu odgovarajućem brojaču.

Nijansa sive se najjednostavnije može odrediti prostom linearnom formulom $i=n/M$, gde je $i$ intenzitet sive nekog piksela, $n$ odgovarajući broj u brojaču, a $M$ najveći od brojeva koji se nalaze u brojačima. Nešto složenija formula koja se često koristi je $$i={\left(\frac{n}{M}\right)}^{\gamma },$$ gde je $\gamma$ pozitivan realan broj. Menjanjem vrednosti $\gamma$ mogu se izraziti neki detalji u budabrot slici koji nisu vidljivi prilikom korišćenja linearne funkcije.

Pseudokod budabrot algoritma izgleda jednostavno:

M = broj odabranih nasumičnih tačaka; 
N = maksimalan broj iteracija;
brojaci = niz od visina_slike x širina_slike brojača;

Ponavljaj M puta {
    c = nasumičan kompleksan broj;
    z = 0;

    Ako c ne pripada Mandelbrotovom skupu {
        Za (i=0; i < N; z++) {
            z = f(z, c);
            Ako je moduo broja z veći od 2 izađi iz petlje;
            Uvećaj brojač koji odgovara tački z za 1;
        }
    }
}

Za svaki piksel C u slici {
    C = T(brojaci[C]);
}

Kvalitet budabrot slike najviše zavisi od tri parametra: dimenzije slike, broja odabranih nasumičnih tačaka i maksimalnog broja iteracija. Kvalitet slike se poboljšava pri uvećavanju maksimalnog broja iteracija kod budabrot algoritma što je prikazano na narednoj figuri.

Broj odabranih nasumičnih tačaka utiče potpuno drugačije na kvalitet slike generisane budabrot algoritmom. Ako algoritam koristi premalo nasumičnih tačaka, tada će postojati mnogo piksela na slici kroz koje nijedna orbita nije „prošla“. Između obojenih piksela će biti previše praznog prostora i budabrot slika će izgledati zrnasto. Ako se broj nasumično odabranih tačaka dovoljno uveća²⁴ tada će kroz većinu piksela proći barem nekoliko orbita, pa će se i prazan prostor između piksela smanjiti (u najboljem slučaju će i u potpunosti nestati). Pritom će i kroz svaki piksel proći mnogo više orbita, pa će svaki od piksela moći i finije da se oboji. Iz navedenog se vidi da optimalan broj nasumično odabranih tačaka mnogo zavisi od dimenzija i rezolucije slike. Kreiranje slika sa većim zoom faktorom je praktično neizvodljivo sa osnovnim budabrot algoritmom, jer se zumiranjem drastično smanjuje verovatnoća da će neka od orbita proći kroz region koji se crta.

Postoji nekoliko jednostavnijih načina da se budabrot algoritam ubrza:

• Pošto se escape time algoritam koristi za određivanje pripadnosti nasumično odabrane tačke Mandelbrotovom skupu, moguće je tom prilikom izračunate članove orbite sačuvati u niz koji će se potom iskoristiti za crtanje orbite. Na taj način se orbita tačaka tačaka računa samo jednom.
• Za ubrzavanje budabrot algoritma može se iskoristi i simetrija Mandelbrotovog skupa: kako konjugavane tačke imaju konjugovane orbite, moguće je izračunati dve orbite po ceni jendne. I opštije, ako se budabrot algoritam primenjuje u slučaju polinoma stepena većeg od dva, tada se može iskoristiti i rotaciona simetrija multibrot skupa.
• Osnovne tehnike optimizacije escape time algoritma su u ovom slučaju veoma korisne: pre ulaska u sam escape time algoritam, lako se može proveriti da li nasumično odabrana tačka pripada glavnoj hiperboličkoj komponenti ili čak hiperboličkoj komponenti perioda dva; a tokom samog escape time algoritma, lako se može proveriti da li je tačka (pre)periodična.

Iako se sa opisanim algoritmom dobijaju grayscale slike, postoji sasvim jednostavan način da se uz pomoć istog algoritma dobiju color slike. Ideja je da se isti region kompleksne ravni nacrta tri puta sa budabrot algoritmom, ali svaki put sa različitim maksimalnim brojem iteracija. Zatim se tri dobijene slike spoje u jednu tako što se svaka od slika interpretira kao jedan od color kanala (R, G ili B). Ovakav način kolorizacije slike se često koristi u astro fotografiji da bi se nevidljivi delovi elektromagnetnog spektra nekog nebeskog objekta pretvorili u vidljive delove spektra. I same budabrot slike kolorizovane na ovaj način podsećaju na nebule²⁵, zbog čega je ova tehnika dobila naziv nebulabrot.

Ako se budabrot algoritam pomeni tako da se umesto orbite tačaka koje ne pripadaju Mandelbrotovom skupu, crtaju orbite tačaka koje pripadaju Mandelbrotovom skupu, dobija se takzvani antibudabrot algoritam, koji takođe može dati zanimljive rezultate.

Metod inverzne iteracije

Metod inverzne iteracije (Inverse iteration method, IMM) je metod crtanja Žulijevog skupa. Za razliku od prethodno opisanih metoda, pri ovoj metodi se posmatraju inverzne iteracije funkcije $f$ za koju crtamo Žulijev skup.

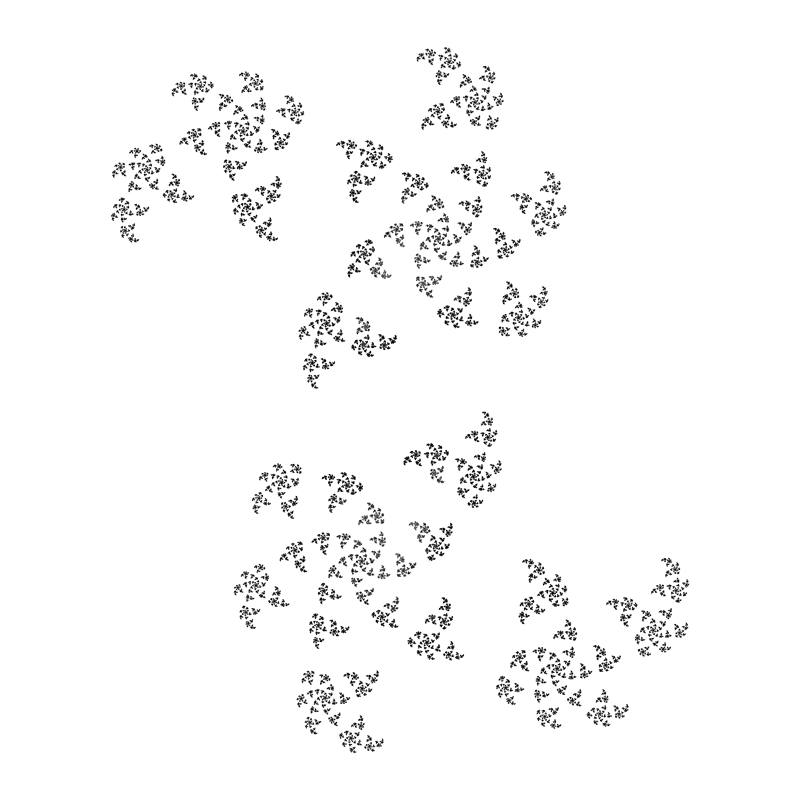
Za ovu metodu je od ključne važnosti naredna teorema:

Teorema 11. Neka je $f$ proizvoljna polinomska funkcija, i neka je $z_0$ periodična odbijajuća tačka funkcije $f$. Tada $z_0$ pripada Žulijevom skupu funkcije $f$.

Dokaz. Pretpostavimo suprotno, da se periodična odbijajuća tačka $z_0$ perioda $n$ nalazi van skupa ${𝒥}_f$. Kako je tačka $z_0$ periodična, ona ne može težiti beskonačnosti pri iteracijama funkcije $f$, pa sledi da se $z_0$ mora nalaziti u interioru ispunjenog Žulijevog skupa ${𝒦}_f$. Neka je sada $r$ poluprečnik, takav da se disk $D$ radijusa $r$ centriran u $z_0$, sadrži ceo u skupu ${𝒦}_f$. Neka je $\lambda$ multiplikator tačke $z_0$. Kako je i $f^n$ polinom, po teoremi 3, postoji $R>0$ takav da za svako $z\in D$ važi $|f^{kn}(z)|<R$ za svako prirodno $k$. Po Košijevoj nejednakosti, važi $\left|\left(f^{nk}\right)\prime \left(z_0\right)\right|<R/r$. Ali, $\left|\left(f^{nk}\right)\prime \left(z_0\right)\right|={\lambda }^k\to \infty$. Kontradikcija. □

Ako posmatramo (lokalnu) inverznu funkciju $f^{-1}$ tada odbijajuće fiksne tačke funkcije $f$ postaju privlačeće fiksne tačke, jer je $\left(f^{-1}\right)\prime \left(z\right)=1/f\prime \left(f^{-1}\left(z\right)\right)$.

Na osnovu teoreme 11 se lako konstruiše IIM algoritam: Neka je $f$ kompleksan polinom stepena $d$. Odaberimo nasumično kompleksan broj $z_0$. Sa $\left\{f^{-1}\left(z_0\right)\right\}$ označimo skup svih rešenja jednačine $f\left(z\right)=z_0$. Kako je $f$ polinom stepena $d$, skup $f^{-1}\left(z_0\right)$ nema više od $d$ elemenata. Kako je Žulijev skup ${𝒥}_f$ sadrži sve privlačeće tačke funkcije $f^{-1}$, sve tačke iz skupa $\left\{f^{-1}\left(z_0\right)\right\}$ su se „približile“ skupu ${𝒥}_f$. Sada opisani postupak možemo ponoviti za sve tačke iz skupa $\left\{f^{-1}\left(z_0\right)\right\}$. Na taj način dobijamo ne više od $d^2$ tačaka koje su još bliže skupu ${𝒥}_f$. Ovaj postupak ponavljamo $N$ puta, čime dobijamo skup od najviše $d^N$ tačaka koje zatim crtamo.

n = maksimalan broj inverznih iteracija;
W = lista od d kompleksnih brojeva;
T = lista kompleksnih brojeva;

funkcija izračunaj_inverzne_iteracije(z, n) {
    ako je n = N {
        dodaj z u T;
        vrati se;
    }

    W = nađi_korene(z);
    za svako w u W {
        izračunaj_inverzne_iteracije(w, n+1);
    }
}

z0 = nasumično odabrana tačka;
izračunaj_inverzne_iteracije(z0, 0);

Za svako z iz T {
    Nacrtaj z na slici;
}

Jasno je da je za implementaciju IIM algoritma potrebna funkcija koja vraća nule kompleksnog polinoma. U slučaju kada je taj polinom drugog stepena (eventualno trećeg ili četvrtog), tada je moguće lako isprogramirati takvu funkciju. Međutim za rešavanje proizvoljnog polinoma stepena većeg od pet, neizbežne su metode numeričke matematike koje mogu biti veoma složene za programiranje. Zbog toga je u takvim situacijama poželjno koristiti biblioteke koje poseduju neophonde numeričke algoritme.

U praksi se ispostavlja da je metoda inverzne iteracije uglavnom veoma brz način za dobijanje kvalitetnih slika Žulijevih skupova. Ipak, postoje polinomske funkcije za koje se malo teže dobijaju kvalitetne slike sa metodom inverzne iteracije. To su funkcije koje poseduju odbijajuće fiksne tačke čiji multiplikator je po modulu veoma blizak jedinici. Takve fiksne tačke sporije privlače ostale tačke pri inverznim iteracijama (videti dokaz teoreme 1), što dovodi do toga da na slici oko njih ostane prazan prostor. Taj problem se može prevazići na nekoliko načina:

• Prvo i najednostavnije rešenje je da se uveća broj inverznih iteracija. Nažalost ovo dovodi do eksponencijalnog uvećavanja vremenske i prostorne složenosti našeg algoritma. Novi problem se može prevazići ako se koriste složeniji tipovi podataka (skupovi) za čuvanje inverznih iteracija.
• Drugo rešenje se sastoji u tome da se za početnu vrednost z0 algoritma ne uzme jedna nasumična tačka, već nekoliko desetina tačaka koje se biraju tako da većina njih bude u ukolini fiksnih tačaka koje prave problem (tj. u okolini fiksnih tačaka čiji multiplikator je po modulu veoma blizak jedinici).

Za detaljniju analizu oba pristupa, pogledati rad [9].

Epilog

Ovde se ovaj tekst o osnovnim informacijama o Žulijevom i Mandelbrotovom skupu završava. Mnogo drugih, zanimljivih, tema vezanih za kompleksnu dinamiku, ostavljeno je za neke naredne tekstove koji će se pojaviti na ovim sajtu. Te teme nisu ušle u ovaj uvodni tekst o kompleksnoj dinamici zbog njihove kompleksnosti. Zainteresovani čitalac lako može sam započeti dublje istraživanje po mnogobrojnoj literaturi. Kao početna tačka u tom istraživanju može mu pomoći spisak korišćene literature koji je naveden u nastavku.

Sve slike koje se pojavljuju u ovom tekstu iscrtane su uz pomoć malog C programa kog sam napisao. Slike su dodatno umanjene i kompresovane uz pomoć Adobe Photoshop programa i odlične opcije Save to Web.

1. Gaston Maurice Julia (1893–1978), francuski matematičar. ↩
2. Benoit B. Mandelbrot (1924–2010), američki matematičar, poljskog porekla. ↩
3. Pierre Joseph Louis Fatou (1878–1929), francuski matematičar i astronom. ↩
4. Funkcija $Z(z)=\frac{1}{2}(z+\frac{1}{z})$ se naziva funkcija Žukovskog. Ova funkcija poseduje mnoga zanimljiva geometrijska svojstva. ↩
5. Felix Hausdorff (1868–1942), nemački matematičar. ↩
6. Topološki prostor je Hausdorfov (T2), ako za svake dve različite tačke $x$ i $y$ tog prostora postoje dva otvorena disjunktna skupa $X$ i $Y$, takva da $x\in X$ i $y\in Y$. ↩
7. Georg Ferdinand Ludwig Philipp Cantor (1845–1918), nemački matematičar. ↩
8. Kantorova lema glasi: U Hausdorfovom prostoru svaki opadajući niz nepraznih kompaktnih skupova ima neprazan presek. ↩
9. Kantorov skup se definiše kao $$𝒞=[0,1]\setminus \bigcup _{n=1}^{\infty }\bigcup _{k=0}^{3^n-1}(\frac{3k+1}{3^{n+1}},\frac{3k+2}{3^{n+1}})$$↩
10. Jednačine koje se tom prilikom dobijaju nije uvek moguće direktno rešiti, već je potrebno koristiti metode numeričke matematike. ↩
11. Kružnice su dve, jer svakoj vrednosti parametra $c$ u opštem slučaju odgvaraju dve vrednosti parametra $\lambda$. ↩
12. Logistička jednačina je (realna) obična diferencijalna jednačina prvog reda $x\prime =(1-x)x$. Ova jednačina (između ostalog) opisuje populaciju neke jedninke koja ima ograničene izvore hrane u svom staništu ↩
13. Reč multibrot je kovanica nastala od reči multiple i Mandelbrot. ↩
14. Lucjan Emil Böttcher (1872–1937), poljski matematičar. ↩
15. Kada bi Žulijev skup bio uniformno naelektrisan, a Fatuov domen vakuum, tada bi elektrostatički potencijal bio dat funkcijom $G$. ↩
16. George Green (1793–1841), engleski matematičar. ↩
17. Skup je lokalno povezan ako svaka njegova njegova tačka ima povezanu okolinu. Postoje skupovi koji su povezani ali nisu lokalno povezani (takav skup je na primer topolška sinusoida). ↩
18. Uvećavanjem broja iteracija, mi dobijamo sve precizniju procenu Žulijevog skupa., a samim tim počinjemo da „vidimo“ sve finije i finije detalje. Ako su detalji sitniji od površine koju pokriva jedan piksel, tada taj piksel ne može verno predstaviti površinu ravni koju pokriva (jer mi bojimo piksel samo na osnovu informacije o jednoj tački koja se nalazi u pomenutoj površini). ↩
19. Boja se može posmatrati kao trodimenzionalni realni vektor koji pripada skupu $[0,1{]}^3$ ↩
20. Prema tome, zajedničke granice među ovim trakama su krive $C,f^{-1}\left[C\right],f^{-2}\left[C\right],\dots$, gde je $C$ kružnica čiji je poluprečnik baš poluprečnik izlaska $R$ koji smo koristili za crtanje. ↩
21. Kako je navedena nejednakost samo procena, postojaće neke tačke za koje ona ne važi. Ponekad se na slici mogu uočiti ovakve tačke kao površine u kojima bojenje nije neprekidno. Tada je dovoljno uvećati parametar $T$ tako da se broj takvih tačaka dovoljno smanji da se ne primete na slici. ↩
22. Ovo su upravo granice traka koje se uočavaju u osnovnom bojenju ↩
23. Sidarta Gautama (5. vek p.n.e) - osnivač budističke religije. ↩
24. U naprednijim algoritmima za crtanje budabrot slika, tačke se ne biraju potpuno nasumično već se tačkama u blizini granice Mandelbrotovog daje prednost pri izboru. Tačkama u blizini granice Mandelbrotovog skupa biće potrebno veoma mnogo iteracija da bi izašle van kružnice izlaska, zbog čega njihove iteracije uvećavaju mnogo brojača. Ovo ima isti efekat kao uvećavanje broja nasumično odabranih tačaka. ↩
25. Maglina (lat. nebula - oblak) je međuzvezdani oblak sačinjen od prašine i gasova. ↩

Literatura

1. Daniel S. Alexander, A History of Complex Dynamics
2. Bodil Branner, The Mandelbrot Set
3. Adrien Douady, John H. Hubbard, Étude dynamique des polynômes complexes
4. Evgeny Demidov, The Mandelbrot and Julia sets Anatomy
5. Kenneth Falconer, Fractal geometry: mathematical foundations and applications
6. Melinda Green, The Buddhabrot Technique
7. John Horgan, Who Discovered the Mandelbrot Set?
8. Linda Keen, Julia Sets
9. Benoit Mandelbrot, The Fractal Geometry of Nature
10. Mark McClure, Basic real and complex dynamics: A computational approach
11. Mark McClure, Inverse iteration algorithms for Julia sets
12. John Milnor, Dynamics in one complex variable
13. Íñigo Quílez, Area of the main bulb of the Mandelbrot set
14. Íñigo Quílez, The symmetry of the Mandelbrot set
15. Linas Vepstas, Renormalizing the Mandelbrot Escape