Complex sphere

It is well known that the set of all points \((x, y)\in\mathbb{R}^2\) which satisfy the equation \[x^2+y^2-1=0\tag{1}\] forms a circle (i.e. a one-dimensional sphere \(S^1\) embedded in \(\mathbb{R}^2\)) centred at the origin and with a radius \(1\).

The following question naturally arises: What complex variety is determined by the polynomial (1)? In other words, what geometric object \(F\subset\mathbb{C}^2\) is determined by the zeros of the complex polynomial \(P(z_1,z_2)=z_1^2+z^2-1.\)

If \(P(z_1, z_2) = 0\) for complex numbers \(z_1 = x+iy\) and \(z_2 = z+iw\), then \[\Re\left(z_1^2+z_2^2\right)=1, \quad \Im\left(z_1^2+z_2^2\right) = 0\] from which follows that \[x^2-y^2+z^2-w^2=1,\\xy+zw=0.\tag{5}\]

Although object \(F\) is a subset of \(\mathbb{C}^2\), we can see \(F\) as a subset of \(\mathbb{R}^4\). Thus, we see that equations (5) give two independent conditions for the coordinates of the set \(F\) in 4-dimensional space. Therefore \(F\) is a surface¹.

As we don't have intuition for four dimensions, we can see this surface only through two-dimensional and three-dimensional sections of \(\mathbb{R}^4\). In the rest of this text, we will determine the sections of the surface \(F\) with three-dimensional space \(w=\lambda\) for \(\lambda\in\mathbb{R}\). In this case equations (5) become \[x^2-y^2+z^2=1+\lambda^2\tag{6}\] \[xy = -\lambda z.\tag{7}\] so we see that \(F\cap\left\{w =\lambda\right\}\) is in the intersection of a hyperbolic paraboloid and a hyperboloid of one sheet. One such intersection is shown in Figure 2.

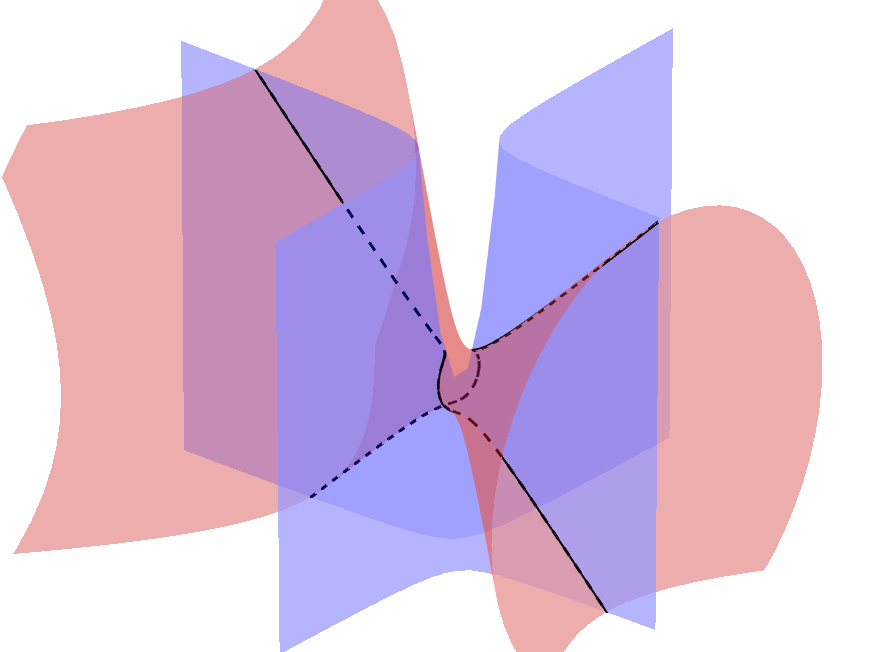
To find the parameterization of this intersection, we can express \(z\) from the equation (7), when \(\lambda\ne 0\). Substituting this into equation (6) we get \(x^2+y^2\left(-1+x^2 /\lambda^2\right) = 1 +\lambda^2\). Solving now for \(y\) gives us \[y =\pm\sqrt{\frac{\lambda^2}{x^2-\lambda^2} -\lambda^2}.\] It follows from equation (7) that \[z=\mp\sqrt{\frac{x^2}{x^2-\lambda^2} -x^2}.\] We expressed both \(y\) and \(z\) coordinates in terms of \(x\) coordinate, so we can parameterize a curve \(F\cap\left\{w =\lambda\right\}\) as follows: \[{\bold r}\left(t\right) =\left(t,\pm\sqrt{\frac{\lambda^2}{t^2-\lambda^2} -\lambda^2},\pm\sqrt{\frac{t^2}{t^2-\lambda^2} -t^2}\right).\tag{8}\]

In the case when \(\lambda=0\), equation (7) represents the union of two planes, so the intersection \(F\cap\left\{w = 0\right\}\) is the union of circle and hyperbola (see Figure 3). The circle that lies in that intersection is actually the circle that polynomial \(x^2+y^2-1\) defines in the real plane.

We can use (8) to find the parameterization of the projection of the whole surface \(F\) to the three-dimensional space. It is enough to parameter \(\lambda\) use as a variable. In that way, we get the following parameterization \[{\bold r}\left(u, v\right) =\left(u,\pm\sqrt{\frac{v^2}{u^2-v^2} -v^2},\pm\sqrt{\frac{u^2}{u^2-v^2}-u^2}\right).\tag{9}\] This surface is shown in Figure 4.

1. The notion of a real surface corresponds to the notion of a complex curve. So a polynomial \(x^2+y^2-1 = 0\) determines the complex curve in \(\mathbb{C}^2\), just as it determines the real curve in \(\mathbb{R}^2\). ↩