Kompleksna sfera

Dobro je poznato da skup svih tačaka $(x,y)\in\mathbb{R}^2$ koje zadovoljavaju jednačinu $$x^2+y^2-1=0\tag{1}$$ čini krug (tj. jednodimenzionu sferu $S^1$ utopljenu u $\mathbb R^2$) centriran u koordinatnom početku i sa poluprečnikom $1$.

Prirodno se nameće sledeće pitanje: Kakvu varijetu određuje polinom iz (1) u $\mathbb C^2$? Drugim rečima, kakav geometrijski objekat $F\subset\mathbb C^2$ određuju nule kompleksnog polinoma $P(z_1,z_2)=z_1^2+z^2-1.$

Ako je $P(z_1,z_2)=0$ za kompleksne brojeve $z_1=x+iy$ i $z_2=z+iw$, tada važe jednakosti $$\begin{aligned}\Re\left(z_1^2+z_2^2\right)&=1, \\ \Im\left(z_1^2+z_2^2\right) &= 0,\end{aligned}$$ odnosno $$x^2-y^2+z^2-w^2=1 \\ xy+zw=0.\tag{5}$$

Iako je $F$ podskup od $\mathbb C^2$, možemo ga na prirodan način "videti" i kao podskup od $\mathbb{R}^4$. Na taj način, vidimo da jednačine (5) zadaju dva nezavisna uslova za koordinate skupa $F$ u 4-dimenzionom prostoru. Prema tome, skup $F$ je površ¹.

Kako nemamo razvijenu intuiciju za četiri dimenzije, ovu površ možemo videti samo kroz dvodimenzionalne i trodimenzionalne preseke. U nastavku ćemo odrediti preseke površi $F$ sa trodimenzionalnim prostorom $w=\lambda$ za $\lambda\in \mathbb{R}$. U tom slučaju jednačine (5) postaju $$x^2-y^2+z^2=1+\lambda^2\tag{6}$$ $$xy=-\lambda z.\tag{7}$$ odakle vidimo da se $F\cap\left\{w=\lambda\right\}$ nalazi u presku jednogranog hiperboloida i hiperboličkog paraboloida. Jedan takav presek je prikazan na slici 2.

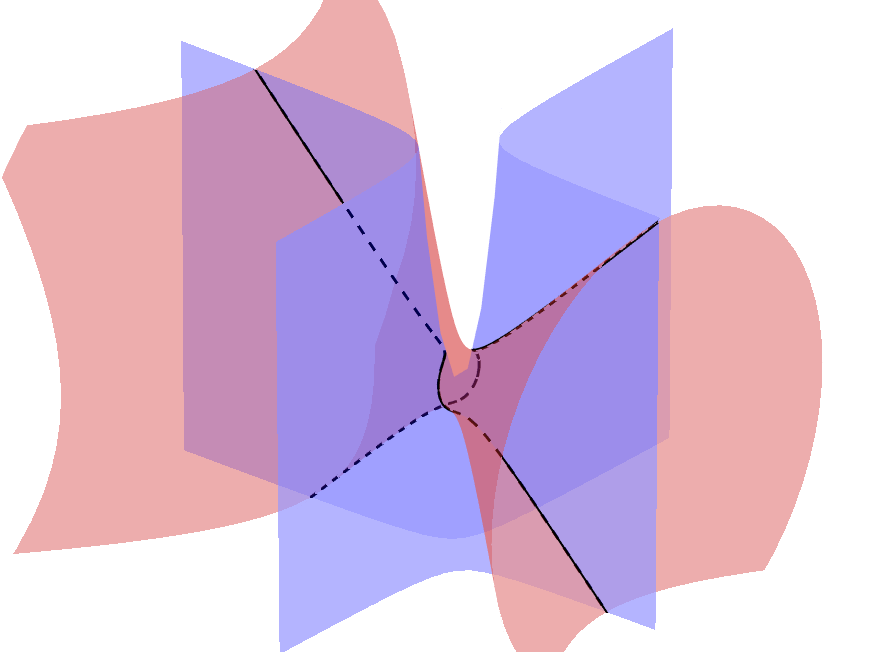
Da bismo našli parametrizaciju ovog preseka, iz jednačine (7) možemo izraziti $z$ kada je $\lambda\ne 0$, odakle zamenom u jednačinu (6) dobijamo da je $x^2+y^2\left(-1+x^2/\lambda^2\right)=1+\lambda^2$. Rešavanjem po $y$ dobijamo da je $$y=\pm\sqrt{\frac{\lambda^2}{x^2-\lambda^2}-\lambda^2}.$$ Iz jednačine (7) sledi da je $$z=\mp\sqrt{\frac{x^2}{x^2-\lambda^2}-x^2}.$$ Na ovaj način smo izrazili $y$ i $z$ koordiante preko $x$ koordinate, zbog čega krivu $F\cap\left\{w=\lambda\right\}$ možemo parametrizovati na sledeći način: $${\bold r}\left(t\right)=\left(t,\pm\sqrt{\frac{\lambda^2}{t^2-\lambda^2}-\lambda^2},\pm\sqrt{\frac{t^2}{t^2-\lambda^2}-t^2}\right).\tag{8}$$

U slučaju kada je $\lambda=0$, jednačina (7) predstavlja uniju dve ravni, pa je je presek $F\cap\left\{w=0\right\}$ unija kruga i hiperbole (videti sliku 3). Krug koji se nalazi u tom preseku je zapravo krug koji određuje polinom $x^2+y^2-1$ u realnoj ravni.

Parametrizaciju (8) možemo iskoristiti da nađemo parametrizaciju projekcije cele površi $F$ na trodimenzionalni prostor. Dovoljno je samo da i parametar $\lambda$ shvatimo kao promenljivu. Na taj način dobijamo sledeću parametrizaciju³ površi $${\bold r}\left(u,v\right)=\left(u,\pm\sqrt{\frac{v^2}{u^2-v^2}-v^2},\pm\sqrt{\frac{u^2}{u^2-v^2}-u^2}\right).\tag{9}$$ Ova površ je prikazana na slici 4.

Deo površi $F$ možemo videti i kao grafik jedne grane kompleksne funkcije $z_2=\sqrt{1-z_1^2}$ kako je prikazano na slici 5. Na toj slici svaka tačka $z_1$ je obojena bojom koju ima tačka $z_2=f(z_1)$ pri standardnom⁴ HSV bojenju kompleksne ravni.

Na ovaj način je određena slika varijeta $F$ pri projekciji $\left(x,y,z,w\right)\mapsto \left(x,y,z\right)$. Zbog simetričnosti jednačina (6) i (7), jasno je da će se ista površ (do na preoznačavanje koordinata) dobiti i pri projekciji $\left(x,y,z,w\right)\mapsto \left(x,z,w\right)$. Međutim, pri projekcijama $\left(x,y,z,w\right)\mapsto \left(x,y,w\right)$ i $\left(x,y,z,w\right)\mapsto \left(y,z,w\right)$ dobijaju se sasvim drugačije površi. Na primer, u prvom slučaju dobijamo parametrizaciju: $${\bold r}\left(u,v\right)=\left(u,\pm\sqrt{v^2-\frac{v^2}{u^2-v^2}},\pm\sqrt{u^2-\frac{u^2}{u^2-v^2}}\right).$$

Za kraj, primetimo da kružnica $S^1$ utopljena u kompleksnu ravan $\mathbb{C}$ ne može biti nula skup ni jednog polinoma iz $\mathbb{C}[z_1]$, iako jeste nula skup u $\mathbb{R}^2$ polinoma iz $\mathbb{R}[x_1,x_2]$.

1. Pojam realne površi odgovara pojmu kompleksne krive. Dakle polinom $x^2+y^2-1=0$ određuje kompleksnu krivu u $\mathbb{C}^2$, baš kao što određuje realnu krivu u $\mathbb R ^2$. ↩
2. Ova parametrizacija nije pogodna za crtnaje u programima zbog računske greške koja se pravi prilikom deljenja kao i zbog neuobičajnog oblika domena (poznati programi za crtanje površi kao što su Wolphram Mathematica, GeoGebra, gnuplot, itd... ne mogu sami da prevaziđu ove probleme). ↩
3. Pri ovom bojenju kompleksne ravni, tačkama se dodeljuje ton boje u zavisnosti argumenta te tačke, a nijansa tog tona (tamnije/svetlije) u zavisnosti od modula te tačke. ↩